- State the following decay mode in the category of allowed, forbidden and Fermi or Gammow-Teller transition
- Fermi transition and allowed
- Fermi transition and second forbidden
- G-T transition and first forbidden
- G-T transition and allowed
- State the following decay mode in the category of allowed, forbidden and Fermi or Gammow-Teller transition
- Fermi transition and allowed
- Fermi transition and second forbidden
- G-T transition and allowed
- G-T transition and third forbidden
- The short wavelength cut-off of the continuous X-ray spectrum from a nickel target is 0.0825 nm. The voltage required to be applied to the X-ray tube must be:
- 0.15 kV
- 1.5 kV
- 15 kV
- 150 kV
- If the Planck's constant were to be zero, then the total energy contained in a box filled with radiation of all frequencies at temperature T would be (where $k$ is Boltzmann constant and $T\ne0$)
- zero
- infinite
- $\frac{3}{2}kT$
- $kT$
- The number of electrons per unit volume in metallic potassium is $1.33\times 10^{28}\: atoms/m^3$ and if each potassium atom donates one electron to the electron gas, its Fermi energy in eV is :
- 4.72
- 3.23
- 2.05
- 1.85
Enhance a problem solving ability in Physics for various competitive and qualifying examinations like GRE, GATE, CSIR JRF-NET, SET, UPSC etc.
Notice
Thursday, 29 December 2016
Problem set 48
Tuesday, 27 December 2016
Problem set 47
- The Lagrangian of a particle moving in a plane is given in Cartesian coordinates as $$L=\dot x\dot y-x^2-y^2$$ In polar coordinates the expression for the canonical momentum (conjugate to the radial coordinate ) is
- $\dot r\sin\theta+r\dot\theta\cos\theta$
- $\dot r\cos\theta+r\dot\theta\sin\theta$
- $2\dot r\cos{2\theta}-r\dot\theta\sin{2\theta}$
- $\dot r\sin{2\theta}+r\dot\theta\cos{2\theta}$
- The Hermite polynomial $H_n(x)$ satisfies the differential equation $$\frac{d^2H_n}{dx^2}-2x\frac{dH_n}{dx}+2nH_n(x)=0$$ . The corresponding generating function $G(x,t)=\sum\limits_{n=0}^{\infty}\frac{1}{n!}H_n(x)t^n$ satisfies the
- $\frac{\partial^2G}{\partial x^2}-2x\frac{\partial G}{\partial x}+2t\frac{\partial G}{\partial t}=0$
- $\frac{\partial^2G}{\partial x^2}-2x\frac{\partial G}{\partial x}-2t^2\frac{\partial G}{\partial t}=0$
- $\frac{\partial^2G}{\partial x^2}-2x\frac{\partial G}{\partial x}+2\frac{\partial G}{\partial t}=0$
- $\frac{\partial^2G}{\partial x^2}-2x\frac{\partial G}{\partial x}+2\frac{\partial^2 G}{\partial x\partial t}=0$
- A sinusoidal signal of peak to peak amplitude 1V and unknown time period is input to the following circuit for 5 seconds duration. If the counter measures a value (3E8)H in hexadecimal then the time period of the input signal is
- 2.5 ms
- 4 ms
- 10 ms
- 5 ms
- For a dynamical system governed by the equation $\frac{dx}{dt}=2\sqrt{1-x^2}$, with $|x|\leq1$,
- $x=-1$ and $x=1$ are both unstable fixed points
- $x=-1$ and $x=1$ are both stable fixed points
- $x=-1$ is an unstable fixed point and $x=1$ is a stable fixed point
- $x=-1$ is a stable fixed point and $x=1$ is an unstable fixed point
- The value of the integral $\int_0^8\frac{1}{x^2+5}dx$, evaluated using Simpson’s $\frac{1}{3}$ rule with $h=2$, is
- 0.565
- 0.620
- 0.698
- 0.736
Substituting $x=r\cos\theta$ and $y=r\sin\theta$ in $L$ \begin{align*} L&={\scriptstyle\left(\dot r\cos\theta-r\dot\theta\sin\theta\right)\left(\dot r\sin\theta+r\dot\theta\cos\theta\right)}\\ &-r^2\cos^2\theta-r^2\sin^2\theta\\ &=\dot r^2\cos\theta\sin\theta+r\dot r\dot\theta\cos^2\theta\\ &-r\dot r\dot\theta\sin^2\theta- r^2\dot\theta^2\cos\theta\sin\theta-r^2\\ &=\frac{1}{2}\dot r^2\sin{2\theta}+r\dot r\dot\theta\cos{2\theta}\\ &-\frac{1}{2} r^2\dot\theta^2\sin{2\theta}-r^2 \end{align*} \begin{align*} p_r=\frac{\partial L}{\partial\dot r}=\dot r\sin{2\theta}+r\dot\theta\cos{2\theta} \end{align*}
Hence, answer is (D)
$\frac{\partial^2G}{\partial x^2}=\sum\limits_{n=0}^{\infty}\frac{1}{n!}\frac{d^2H_n}{d x^2}t^n$, $\frac{\partial G}{\partial x}=\sum\limits_{n=0}^{\infty}\frac{1}{n!}\frac{dH_n}{d x}t^n$, $2t\frac{\partial G}{\partial t}=2n\sum\limits_{n=0}^{\infty}\frac{1}{n!}H_n( x)t^n$ \begin{align*} &\frac{\partial^2G}{\partial x^2}-2x\frac{\partial G}{\partial x}+2t\frac{\partial G}{\partial t}\\ &{\scriptstyle =\sum\limits_{n=0}^{\infty}\frac{1}{n!}\left(\frac{d^2H_n}{d x^2}-2x\frac{1}{n!}\frac{dH_n}{d x}+2n\frac{1}{n!}H_n( x)\right)t^n}\\ &=0 \end{align*} Hence, answer is (A)
In general n-bit counter counts $2^n$ numbers in a sequence ranging from 0 to $2^n-1$ and the counter cycles through the same sequence of numbers continuously so long as there is an incoming clock pulse. For one complete cycle we require $2^n-1$ pulses.
If $T$ is time period of a pulse then time required for one complete cycle of counts = $T\times(2^n-1)$.
Now, to count a decimal number $N$ we require $N$ pulses. This can be seen from a table below for a 2-bit counter.
| Input pulse | Count | decimal equivalent |
| 0 | 00 | 0 |
| 1 | 01 | 1 |
| 2 | 10 | 2 |
| 3 | 11 | 3 |
The decimal equivalent of $(3E8)_H={\scriptstyle 3\times16^2+14\times16^1+8\times16^0}=1000$ Hence, 1000 pulses of time period $T$ will be required to count the number $(3E8)_H$ in 5 seconds. $$5 \:sec=1000\times T$$ $$T=\frac{5}{1000}=5\:msec$$
Hence, answer is (D)
As $f(-1)=0$, x=-1 is a fixed point.
As $f(1)=0$, x=1 is a fixed point. $$f'(x)=\frac{-2x}{\sqrt{1-x^2}}$$
As $f'(-1)=\frac{2}{0}=\infty > 0$, $x=-1$ is a unstable point.
As $f'(1)=\frac{-2}{0}=-\infty < 0$, $x=1$ is a stable point.
Hence, answer is (C)
Hence, answer is (A)
Monday, 26 December 2016
Problem set 46
- Parity non-conversion was established in $\beta$-decay when it was observed that from $Co^{60}$ nuclei:
- Electrons were emitted equally in all directions
- More electrons were emitted in direction opposite to that of magnetic field
- Electrons were not emitted in any direction
- More electrons were emitted perpendicular to the direction of magnetic field
- According to the liquid drop model, the occurrence of fission is due to competition between :
- Surface energy term and symmetry energy term
- Surface energy term and Coulomb energy term
- Volume energy term and surface energy term
- Volume energy term and Coulomb energy term
- Binding energy difference in mirror nuclei can be understood using Coulomb energy difference. This indicates that :
- Nuclear force is spin dependent
- Nuclear force is strong force
- Nuclear force is as strong as Coulomb force
- Nuclear force is charge independent
- Give the approximate values for the corresponding lifetimes of hadronic decay, electromagnetic decay and weak decay
- $10^{-9}\:sec$, $10^{-6}\:sec$, $10^{-3}\:sec$
- $10^{-12}\:sec$, $10^{-9}\:sec$, $10^{-6}\:sec$
- $10^{-15}\:sec$, $10^{-13}\:sec$, $10^{-6}\:sec$
- $10^{-23}\:sec$, $10^{-18}\:sec$, $10^{-10}\:sec$
- Based on the additive quantum numbers such as Lepton number, Baryon number, charge of the particle and Isospin, indicate the following nuclear reaction cannot be induced with the following combination: $$n\rightarrow p+e^-+\nu_e^-$$
- Q, B are conversed, but $I_3$, L are not conserved
- Q, B, L are conversed, but $I_3$ is not conserved
- Q, B, $I_3$ are conversed, but L is not conserved
- B, $I_3$, L are conversed, but Q is not conserved
Hence, answer is (B)
Hence, answer is (B)
This indicates that nuclear force is charge independent.
Hence, answer is (D)
(D) $10^{-23}\:sec$, $10^{-18}\:sec$, $10^{-10}\:sec$
| $n\rightarrow p+e^-+\nu_e^-$ | ||
| Q | $0\rightarrow 1-1+0$ | Conserved |
| B | $1\rightarrow 1+0+0$ | Conserved |
| L | $0\rightarrow 0+1-1$ | Conserved |
| $I_3$ | $-\frac{1}{2}\rightarrow \frac{1}{2}$ | Not conserved |
Hence, answer is (B)
Sunday, 25 December 2016
Problem set 45
- A plane electromagnetic wave is traveling along the positive z-direction. The maximum electric field along the x-direction is 10 V/m. The approximate maximum values of the power per unit area and the magnetic induction $B$, respectively, are
- $3.3\times 10^{-7} watts/m^2$ and 10 tesla
- $3.3\times 10^{-7} watts/m^2$ and $3.3\times 10^{-8} $ tesla
- $0.265 watts/m^2$ and $10$ tesla
- $0.265 watts/m^2$ and $3.3\times 10^{-8} $ tesla
- A particle moves in one dimension in the potential $V=\frac{1}{2}k(t)x^2$, where $k(t)$ is a time dependent parameter. Then $\frac{d}{dt}\left < V\right >$, the rate of change of the expectation value $\left < V\right >$ of the potential energy, is
- $\frac{1}{2}\frac{dk}{dt}\left < x^2\right > +\frac{k}{2m}\left < xp+px\right >$
- $\frac{1}{2}\frac{dk}{dt}\left < x^2\right > +\frac{1}{2m}\left < p^2\right >$
- $\frac{k}{2m}\left < xp+px\right >$
- $\frac{1}{2}\frac{dk}{dt}\left < x^2\right >$
- Consider three inertial frames of reference A, B and C. The frame B moves with a velocity $c/2$ with respect to $A$, and $C$ moves with velocity $c/10$ with respect to B in the same direction. The velocity of C as measured in A is
- $\frac{3c}{7}$
- $\frac{4c}{7}$
- $\frac{c}{7}$
- $\frac{\sqrt{3}c}{7}$
- Suppose the yz-plane forms a chargeless boundary between two media of permittivities $\epsilon_{left}$ and $\epsilon_{right}$ where $\epsilon_{left}:\epsilon_{right}=1:2$. If the uniform electric field on the left is $\vec E_{left}=c\left(\hat i+\hat j+\hat k\right)$ (where $c$ is constant), then the electric field on the right $\vec E_{right}$ is
- $c\left(2\hat i+\hat j+\hat k\right)$
- $c\left(\hat i+2\hat j+2\hat k\right)$
- $c\left(\frac{1}{2}\hat i+\hat j+\hat k\right)$
- $c\left(\hat i+\frac{1}{2}\hat j+\frac{1}{2}\hat k\right)$
- Which of the following transformations $\left(V,\vec A\right)\rightarrow \left(V',\vec A'\right)$ of electrostatic potential $V$ and the vector potential $\vec A$ is a gauge transformation?
- $\left(V'=V+ax,\vec A'=\vec A+at\hat k\right)$
- $\left(V'=V+ax,\vec A'=\vec A-at\hat k\right)$
- $\left(V'=V+ax,\vec A'=\vec A+at\hat i\right)$
- $\left(V'=V+ax,\vec A'=\vec A-at\hat i\right)$
The power per unit area transported by the electromagnetic waves is given \begin{align*} I&=c\epsilon_0E_0^2\\ &=3\times 10^8\times8.854\times10^{-12}\times10^2\\ &=0.265 watts/m^2 \end{align*}
Magnetic induction \begin{align*} B&=\frac{1}{c}E_0\\ &=\frac{1}{3\times10^{-8}}\times10\\ &=3.3\times 10^{-8} \: tesla \end{align*}
Hence, answer is (D)
$$\frac{d\left <\hat A\right >}{dt}=\left < \frac{\partial \hat A}{\partial t}\right > +\frac{i}{\hbar}\left < \left[\hat H,\hat A\right]\right > $$ \begin{align*} &\frac{d\left < V\right >}{dt}={\textstyle\left < \frac{\partial V}{\partial t}\right > +\frac{i}{\hbar}\left < \left[\frac{p^2}{2m}+V, V\right]\right >}\\ &={\textstyle\left < \frac{\partial V}{\partial t}\right > +\frac{i}{2m\hbar}\left < \left[p^2,V\right]\right > }\\ &={\scriptstyle\left < \frac{\partial \left(\frac{1}{2}k(t)x^2\right)}{\partial t}\right > +\frac{i}{2m\hbar}\left < \left[p^2,\frac{1}{2}k(t)x^2\right]\right > }\\ &={\textstyle\frac{1}{2}\frac{dk}{d t}\left < x^2\right > +\frac{ik}{4m\hbar}\left < \left[p^2,x^2\right]\right > }\\ &={\textstyle\frac{1}{2}\frac{dk}{d t}\left < x^2\right > }\\ &{\scriptstyle+\frac{ik}{4m\hbar}\left < xp\left[p,x\right]+\left[p,x\right]p+p\left[p,x\right]x+\left[p,x\right]xp\right > }\\ &={\textstyle\frac{1}{2}\frac{dk}{d t}\left < x^2\right > +\frac{ik}{4m\hbar}\left < -2i\hbar xp-2i\hbar px \right > }\\ &={\textstyle\frac{1}{2}\frac{dk}{d t}\left < x^2\right > +\frac{k}{2m}\left < xp+ px \right > } \end{align*}
Let $V$ be the velocity of frame $B$ with respect to frame A, $u_x$ be the velocity of frame C with respect to frame A, and $u_x'$ be the velocity of frame C with respect to frame B, then we have $$u_x'=\frac{u_x-V}{1-u_xV/c^2}$$and $$u_x=\frac{u_x'+V}{1+u_x'V/c^2}$$ \begin{align*} u_x&=\frac{u_x'+V}{1+u_x'V/c^2}\\ &=\frac{\frac{c}{10}+\frac{c}{2}}{1+\frac{c}{10}\frac{c}{2}\frac{1}{c^2}}=\frac{4}{7}c \end{align*}
Hence, answer is (B)
Using relation $$E_{left}\epsilon_{left}\cos{\theta_1}=E_{right}\epsilon_{right}\cos{\theta_2}$$ where, $\theta_1$ is the angle between $\vec E_{left}$ and the vector normal to the yz-plane and $\theta_2$ is the angle between $\vec E_{right}$ and the vector normal to the yz-plane. The vector normal to yz-plane is $\hat i$
Using $\epsilon_{left}:\epsilon_{right}=1:2$ in above equation $$E_{left}\cos{\theta_1}=2E_{right}\cos{\theta_2}\quad--(1)$$ Magnitude of $\vec E_{left}$ is given by $$E_{left}=\sqrt{c^2+c^2+c^2}=\sqrt{3}c$$ Let us find angle $\cos{\theta_1}$ \begin{align*} \cos{\theta}&={\textstyle\frac{a_1b_1+a_2b_2+a_3b_3}{\sqrt{a_1^2+a_2^2+a_3^2}\sqrt{b_1^2+b_2^2+b_3^2}}}\\ &=\frac{c}{\sqrt{3c^2}\sqrt{1}}=\frac{1}{\sqrt{3}} \end{align*} Hence, equation (1) becomes $$\sqrt{3}c\times\frac{1}{\sqrt{3}}=2E_{right}\cos{\theta_2}$$ $$E_{right}\cos{\theta_2}=\frac{c}{2}$$ One cane verify that $E_{right}=c\left(\hat i+2\hat j+2\hat k\right)$ satisfies the above condition. For this vector find $E_{right}$ and $\cos\theta_2$.
Hence, answer is (B)
The general gauge transformation of electrostatic potential $V$ and the vector potential $\vec A$ is given by the equations $$ V'=V-\frac{\partial f}{\partial t}$$ $$\vec A'=\vec A+\nabla f$$ In all options, we have, $V'=V+ax$. This implies $$-\frac{\partial f}{\partial t}=ax$$ Hence, $f=-atx$
Hence, $\nabla f=-at\hat i$
Hence, we have, $\left(V'=V+ax,\vec A'=\vec A-at\hat i\right)$
Hence, answer is (D)
Thursday, 22 December 2016
Problem set 44
- Three polarizers P1, P2 and P3 are arranged as shown in figure. Optical axis of P1 and P3 are perpendicular to one another while the axis of P2 makes an angle $\theta$ with that of P1. If a beam of ordinary light of intensity I0 is incident normally on P1, then the intensity of light emerging from P3 is :
- 0
- $\frac{I_0}{8}\sin^2{2\theta}$
- $\frac{I_0}{2}$
- $\frac{I_0}{4}\sin^2{2\theta}$
- There is no infrared absorption for nitrogen molecule because:
- its polarizability is zero
- it has no vibrational levels
- it has no rotational levels
- its dipole moment is zero
- In the first order Stark effect in hydrogen atom the ground state split into :
- 2 levels
- 3 levels
- 4 levels
- does not split
- According to Hund's rule, the ground state of Si (atomic number 14) atom is
- $^1P_1$
- $^3P_0$
- $^3P_3$
- $^3D_3$
- A source with bandwidth of $10^{-3}\:nm$ centered about $\lambda=500\:nm$ has a coherence length
- 0.25 m
- 2.5 $\mu$m
- 25 cm
- 2.5 m
When ordinary light falls on the polarizer, then the intensity of light passed through polarizer is one half the intensity of unpolarized light
Hence, for polarizer $P_1$, we have $$I_1=\frac{I_0}{2}$$ For polarizer $P_2$, according to Malus law $$I_2=I_1\cos^2\theta=\frac{I_0}{2}\cos^2\theta$$ For polarizer $P_3$, according to Malus law \begin{align*} I_3&=\frac{I_2}{2}\cos^2{(\frac{\pi}{2}\theta)}\\ &=\frac{I_0}{2}\cos^2\theta\cos^2{(\frac{\pi}{2}\theta)}\\ &=\frac{I_0}{2}\cos^2\theta\sin^2{(\theta)}\\ &=\frac{I_0}{8}\left(2\cos\theta\sin{(\theta)}\right)^2\\ &=\frac{I_0}{8}\sin^2{2\theta} \end{align*} Hence, answer is (B)
Hence answer is (D)
Hence, answer is (D)
For $3p^2$ electrons $m_{l_1}=+2$, $m_{l_2}=+1$, hence $L=2+1=3$
Hence, $J=L-S=0$
term symbol is $^3P_0$
Hence, answer is (B)
Tuesday, 20 December 2016
Problem set 43
- A positive clamping circuit is one that clamps:
- The positive extremity of the signal to the zero level
- The positive extremity of the signal to a positive dc voltage
- The negative extremity of the signal to the zero level
- The negative extremity of the signal to a positive dc voltage
- Positive clamping occurs when negative peaks raised or clamped to ground or on the zero level i.e., it pushes the signal upwards so that negative peaks fall on the zero level.
- Negative clamping occurs when positive peaks raised or clamped to ground or on the zero level i.e., it pushes the signal downwards so that the positive peaks fall on the zero level.
- A positive logic NAND gate performs same as the negative logic:
- XOR gate
- OR gate
- AND gate
- NOR gate
- If $C=0.1\mu F$, $R=3.25k\Omega$ in a phase shift oscillator feedback circuit, then the frequency of oscillation is:
- 200 kHz
- 100 Hz
- 200 Hz
- 100 kHz
- Load regulation is determined by :
- Changes in load current and output voltage
- Changes in load current and input voltage
- Changes in load resistance and input voltage
- Changes in Zener current and load current
- A carrier is simultaneously modulated by two sine waves with modulation indices of 0.3 and 0.4; then the total modulation index is :
- 1
- 0.1
- 0.5
- 0.35
A circuit that places either the positive or negative peak of a signal at a desired D.C level is known as a clamping circuit. A clamping circuit introduces (or restores) a D.C level to an A.C signal. Thus a clamping circuit is also known as D.C restorer, or D.C reinserted or a baseline stabilizer. The following are two general types of clamping.
In both cases the shape of the original signal has not changed, only there is vertical shift in the signal
Hence, answer is (C).
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
| 1 | 1 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 0 | 1 |
Hence, answer is (D)
Hence, answer is (C)
Hence, answer is (A)
Hence, answer is (C)
Sunday, 18 December 2016
Problem set 42
- The input signal for the equivalent circuit shown below can have a frequency between 10 Hz and 50 kHz, then the value of the coupling capacitor is:
- $1\mu F$
- $10 pF$
- $1 pF$
- $10\mu F$
- In a 3-input OP-AMP summing amplifier shown below, the output voltage $(v_0)$ is
- -3 V
- +3 V
- +6 V
- -9 V
- In the circuit given below what is the approximate ac voltage across the output resistor:
- 15 mV
- 150 mV
- 15 $\mu$V
- 15 V
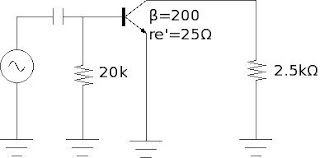
- The input impedance $(Z_{in(total)})$ of the common-emitter amplifier given below is:
- $5k\Omega$
- $4k\Omega$
- $2k\Omega$
- $20k\Omega$
- The load voltage in a Zener circuit shown below with $V_z=15V$ is approximately
- 15 V
- 10 V
- 14.3 V
- 15.7 V
transistor base impedance $=\beta r_e=200\times25=5k\Omega$ $$Z_{in(total)}=20||\beta r_e$$ \begin{align*} \frac{1}{Z_{in(total)}}&=\frac{1}{20}+\frac{1}{\beta r_e}\\ &=\frac{1}{20}+\frac{1}{5}=\frac{1}{4} \end{align*} $$Z_{in(total)}=4k\Omega$$ Hence, answer is (B)
Friday, 16 December 2016
Problem set 41
- In the op-amp circuit shown in the figure, $V_i$ is a sinusoidal input signal of frequency $10 Hz$ and $V_0$ is the output signal. The magnitude of the gain and the phase shift, respectively, close to values
- $5\sqrt{2}$ and $\pi/2$
- $5\sqrt{2}$ and $-\pi/2$
- 10 and zero
- 10 and $\pi$
- The logic circuit shown in the figure below implements the Boolean expression
- $y=\overline{A\cdot B}$
- $y=\bar{A}\cdot \bar{B}$
- $y=A\cdot B$
- $y=A+ B$
- A time varying signal $V_{in}$ is fed to an op-amp circuit with output signal $V_0$ as shown in the figure below. The circuit implements a
- high pass filter with cutoff frequency 16Hz
- high pass filter with cutoff frequency 100 Hz
- low pass filter with cutoff frequency 16Hz
- low pass filter with cutoff frequency 100 Hz
- In the following circuit the current through the load resistance is:
- 10 mA
- 1 mA
- 5 mA
- 0.5 mA
- In the following clipping circuit, the clipping level is:
- + 25 V
- - 25 V
- - 5 V
- + 5 V
Hence, answer is (A)
Hence, answer is (C)
Hence, answer is (D)
Wednesday, 14 December 2016
Problem set 40
- If superconducting lead has critical temperature of 7.26 K at zero magnetic field and a critical field of $8\times10^5 A/m$ at 0K, the critical field at 5K is :
- $6.3\times 10^5 A/m$
- $2.5\times 10^5 A/m$
- $4.2\times 10^5 A/m$
- $1.5\times 10^5 A/m$
- The ratio of the sizes (in terms of radii) of $^{208}_{82}Pb$ and $^{26}_{12}Mg$ nuclei is approximately:
- 2
- 4
- $2\sqrt{2}$
- 8
- What is the energy of a gamma radiation backscattered at an angle $180^o$, if the incident energy is 10 MeV?
- 10 MeV
- 5 MeV
- 0.511 MeV
- 0.25 MeV
- Ionisation chamber is effectively used for the measurement of :
- Radiation
- Radiation Dose
- strength of radiation
- Energy of radiation
- A satisfactory quenching gas in G.M. tube must have the following property:
- Ionisation potential should be equal to the main counting gas in the tube
- Ionisation potential should be higher than that of main counting gas in the tube
- It must have very narrow ultraviolet absorption bands
- When in excited state it must prefer to dissociate rather than to de-excite by the emission of photon
$T=5K$ Temperature at which critical field of lead is to be found outside
$T_c=7.26 K$ Critical temperature of lead
\begin{align*} H_{c_T}&=H_{c_0}\left(1-\left(\frac{T}{T_c}\right)^2\right)\\& =8\times10^5\left(1-\left(\frac{5}{7.26}\right)^2\right)\\ &=4.2\times10^5 A/m \end{align*}
Hence, answer is (B)
1: Its ionisation potential should be less than the main gas
2: It should be complex and prone to dissociation rather than de-excite by photon emission
3: It should have sharp and intense absorption band in UV so that it quickly dissociates by absorbing undesired UV causing spurious discharge.
Monday, 12 December 2016
Problem set 39
- A state of a system with spherically symmetric potential has zero uncertainty in simultaneous measurement of operator $L_x$ and $L_y$. Which of the following statement is true?
- The state must be $l=0$ state
- Such a state can never exist as operators $L_x$ and $L_y$ do not commute
- The state has $l=1$ with $m=0$
- The state cannot be an eigenstate of $L^2$ operator
- The wave function for identical fermions is antisymmetric under particle exchange. Which of the following is a consequence of this property?
- Heisenberg's uncertainty principle
- Bohr correspondence principle
- Bose-Einstein condensation
- Pauli exclusion principle
- The spin part of two electron wave function is described as a triplet state. The space part of the wave function is given by ($\psi_1$ and $\psi_2$ are two different functions):
- $\psi_1(r_1)\psi_2(r_2)$
- $\psi_1(r_1)\psi_2(r_2)-\psi_2(r_1)\psi_1(r_2)$
- $\psi_1(r_1)\psi_2(r_2)+\psi_2(r_1)\psi_1(r_2)$
- $\psi_1(r_1)\psi_1(r_2)+\psi_2(r_1)\psi_1(r_2)$
- A transition in which one photon is radiated by the electron in a hydrogen atom when the electron's wave function changes from $\psi_1$ to $\psi_2$ is forbidden if $\psi_1$ and $\psi_2$
- have opposite parity
- are both spherically symmetrical
- are orthogonal to each other
- are zero at the center of the atomic nucleus
- The puzzle of magic numbers for nuclei was resolve by :
- introducing hard-core potential
- introducing Yukawa potential for shell model
- introducing tensor character to nuclear force
- introducing spin-orbit part in the nuclear potential
Hence, answer is (A)
For $M_s=0$ we must have either $m_{s1}=\frac{1}{2}$ and $m_{s2}=-\frac{1}{2}$ or $m_{s1}=-\frac{1}{2}$ and $m_{s2}=\frac{1}{2}$
For $M_s=+1$ we must have $m_{s1}=+\frac{1}{2}$ and $m_{s2}=+\frac{1}{2}$
Hence, we have three possible spin eigenfunctions $$\phi\left(+\frac{1}{2},+\frac{1}{2}\right)$$ $$\frac{1}{\sqrt{2}}\left[\phi\left(+\frac{1}{2},-\frac{1}{2}\right)+\phi\left(-\frac{1}{2},+\frac{1}{2}\right)\right]$$ $$\phi\left(-\frac{1}{2},-\frac{1}{2}\right)$$ All these functions are symmetric. However, total wavefunction must be antisymmetric. Hence, space part must be antisymmetric.
Hence, answer is (B) i.e. $\psi_1(r_1)\psi_2(r_2)-\psi_2(r_1)\psi_1(r_2)$
| 1. | Principal quantum number | : | $\Delta n=$ anything |
| 2. | Orbital angular momentum | : | $\Delta l = \pm1$ |
| 3. | Magnetic quantum number | : | $\Delta m_l = 0, \pm1$ |
| 4. | Spin | : | $\Delta s = 0$ |
| 5. | Total angular momentum | : | $\Delta j = 0, \pm 1,{\scriptstyle \text{ but} j = 0 \nrightarrow j= 0}$ |
A. FALSE: It's not related to the selection rules.
B. TRUE: If both initial and final states have spherically symmetrical wave functions, then they have the same angular momentum. $l = 0 \rightarrow l = 0$ is forbidden as $\Delta l=0$ in this case.
C. FALSE: In any transition, eigenstates should always be mutually orthogonal.
D. FALSE: Eigenstates zero at the center $\Rightarrow l> 0$ could change, for example from 3 to 2. This is allowed.
Hence, answer is (B)
Saturday, 10 December 2016
Problem set 38
- Merit of a solar cell or fill factor is
- $I_mV_m/I_{SC}V_{OC}$
- $I_mV_{OC}/I_{SC}V_{m}$
- $I_{SC}V_{OC}/I_{m}V_{m}$
- $I_{SC}V_{m}/I_{m}V_{OC}$
- The resonant frequency of a Heartly oscillator with $L_1=12\mu H$, $L_2=8\mu H$ and $C=1000PF$ is:
- 1.12 MHz
- 11.2 MHz
- 11.2 kHz
- 112 kHz
- In an open loop differential operational amplifier having gain of $A=2\times10^5$ receives inputs as at non-inverting terminal $5\mu V$ and at inverting terminal $-7\mu V$, then the output is:
- 2.4 V
- 0.24 V
- 2.4 mV
- 2.4 $\mu$V
- The number of Full-adders and Half-adders required to addd 16-bit numbers is
- 1 HA and 15 FA
- 8 HA and 08 FA
- 16 HA and 0 FA
- 4 HA and 12 FA
- Sum of all the three inputs will appear as output from:
- A 3-input NAND gate followed by an inverter
- A 3-input XOR gate followed by an inverter
- A 3-input NOR gate followed by an inverter
- An inverter followed by 3-input NOR gate
Hence, answer is (A)
Thursday, 8 December 2016
Problem Set 37
- The LS configurations of the ground state of $^{12}Mg$, $^{13}Al$, $^{17}Cl$ and $^{18}Ar$ are, respectively,
- $^3S_1$, $^2P_{1/2}$, $^2P_{1/2}$ and $^1S_{0}$
- $^3S_1$, $^2P_{3/2}$, $^2P_{3/2}$ and $^3S_{1}$
- $^1S_0$, $^2P_{1/2}$, $^2P_{3/2}$ and $^1S_{0}$
- $^1S_0$, $^2P_{3/2}$, $^2P_{1/2}$ and $^3S_{1}$
- The frequency dependent dielectric constant of a material is given by $$\epsilon(\omega)=1+\frac{A}{\omega_0^2-\omega^2-i\omega\gamma}$$ where $A$ is a positive constant, $\omega_0$ the resonant frequency and $\gamma$ the damping coefficient. For an electromagnetic wave of angular frequency $\omega < < \omega_0$, which of the following is true? (Assume that $\frac{\gamma}{\omega_0} < < 1$.)
- There is negligible absorption of the wave
- The wave propagation is highly dispersive
- There is strong absorption of the electromagnetic wave
- The group velocity and the phase velocity will have opposite sign
- The state diagram corresponding to the following circuit is
- Consider a random walker on a square lattice. At each step the walker moves to a nearest neighbour site with equal probability for each of the four sites. The walker starts at the origin and takes 3 steps. The probability that during this walk no site is visited more than once is
- 12/27
- 27/64
- 3/8
- 9/16
- A canonical transformation $(p,q)\rightarrow(P,Q)$ is performed on the Hamiltonian $H=\frac{1}{2m}p^2+\frac{1}{2}m\omega^2q^2$ via the generating function $F=\frac{1}{2}m\omega q^2\cot{Q}$. If $Q(0)=0$, which of the following graphs shows schematically the dependence of $Q(t)$ on $t$?
Electronic configuration of $^{12}Mg$ is $1s^22s^22p^63s^2$
There are two 3s electrons with $s_1=\frac{1}{2}$ and $s_2=\frac{1}{2}$. Hence, $S=1$ and $2S+1=3$
For two 3s electrons each with $l=0$, $m_l=0$. Hence, $L=0$
$J=L+S=0$. Hence, term symbol for $^{12}Mg$ is $^1S_0$
For, $^{13}Al$, electronic configuration is $1s^22s^22p^63s^23p^1$
$S=\frac{1}{2}$, $2S+1=2$, $L=1$, $J=L-S=1-\frac{1}{2}=\frac{1}{2}$ (less than half-filled)
Hence, term symbol for $^{13}Al$ is $^2P_{1/2}$
Hence, answer is (C).
Hence, answer is (A)
Now, suppose the flip-flop is in state ⓪ i.e. $A=0$. If the $x, y$ inputs are $1,1$ then output $A$ will remain 0 i.e. the state remains same ⓪.
Hence, option (D) is correct
During first step of random walk the probability that during this walk no site is visited more than once is 1
During second step of random walk the probability that during this walk no site is visited more than once is 3/4, because there are 3 sites which are unvisited and each site has probability 1/4
Similarly, during third step of random walk the probability is 3/4
Hence, the probability that during first, second and third step, no site is visited more than once is $$p=1\times\frac{3}{4}\times\frac{3}{4}=\frac{9}{16}$$
Hence, answer is (D)
$\frac{\partial F}{\partial q}=p$ gives $$m\omega q\cot{Q}=p$$
$\frac{\partial F}{\partial Q}=-P$ gives $$-\frac{1}{2}m\omega q^2 \text{ cosec}^2Q=-P$$ $$q^2=\frac{2P}{m\omega \text{ cosec}^2Q}$$ \begin{align*} H'&={\scriptstyle\frac{1}{2m}m^2\omega^2q^2\cot^2Q+\frac{1}{2}m\omega^2\frac{2P}{m\omega \text{ cosec}^2Q}}\\ &={\scriptstyle\frac{1}{2m}m^2\omega^2\frac{2P}{m\omega \text{ cosec}^2Q}\cot^2Q+\frac{1}{2}m\omega^2\frac{2P}{m\omega \text{ cosec}^2Q}}\\ &=P\omega\cos^2Q+P\omega\sin^2Q\\ &=P\omega \end{align*} Using canonical equation $\dot Q=\frac{\partial H'}{\partial P}$ we have $$\frac{dQ}{dt}=\omega$$ $$Q=\omega t+c$$ where $c$ in integrating constant. But at $t=0$, $Q(t)=0$, hence, $c=0$ $$Q=\omega t$$ Which is equation of straight line.
Hence, answer is (D)
Tuesday, 6 December 2016
Problem set 36
- For a finite square well potential in one dimension:
- It is possible that no bound state exits
- There is always at least one bound state
- Bound states have degeneracy = 2
- Energy levels of bound states are equally spaced
- A particle with spin $\frac{1}{2}$ is in state with eigenstate of $S_z$. Then the expectation values of $S_x$, $S_x^2$ in this state are given by:
- $-\frac{\hbar}{2}$, $\frac{1}{4}\hbar$
- $0$, $\frac{3}{4}\hbar^2$
- $\frac{\hbar}{2}$, $\frac{3}{4}\hbar^2$
- $0$, $\frac{1}{4}\hbar^2$
- The differential cross-section for a central potential is equal to
- $f(\theta,\phi)$
- $f^*(\theta,\phi)$
- $f^*(\theta,\phi)f(\theta,\phi)$
- $|f(\theta,\phi)|$
- The de Broglie wavelength of a helium atom at 300 K is 0.06 $A^o$. The de Broglie wavelength of neon atom (5 times heavier than helium) at 600 K will be:
- 6 Å
- 0.06 Å
- $0.06\times\sqrt{10}$Å
- $\frac{0.06}{\sqrt{10}}$Å
- If a charged particle $q$ moves along a circle of radius $r=100mm$ in a uniform magnetic field $B=10mT$, then the period of revolution of the particle $(m_p=1.67\times10^{-27}kg, q=1.6\times10^{-19}C)$
- 6.55 ms
- 6.55 $\mu$s
- 6.55 ns
- 3$\mu$s
Hence, answer is (D)
Sunday, 4 December 2016
Problem set 35
- The energy of formation of a vacancy in copper is $1eV$. The number of vacancies per mole below its melting point $1356^oK$ is:
- $1.15\times10^{20}$
- $4\times10^{20}$
- $2\times10^{20}$
- $3.30\times10^{20}$
- A system is known to be in a state described by the wave function $$\psi(\theta,\phi)=\frac{1}{\sqrt{30}}\left[5Y_4^0+5Y_6^0+25Y_6^3\right]$$ where $Y_l^m$ are spherical harmonics. The probability of finding the system in a state with $m=0$ is :
- Zero
- $\frac{6}{\sqrt{30}}$
- $\frac{6}{30}$
- $\frac{13}{15}$
- For attractive one-dimensional delta function potential situated at $x=0$, the wave function of the bound state is given by:
- $\psi(x)=e^{-\alpha x}$
- $\psi(x)=e^{-\alpha |x|}$
- $\psi(x)=e^{-\alpha x^2}$
- $\psi(x)=\sin{\alpha x}$
- A one-dimensional simple harmonic oscillator with generalized coordinate $q$ is subjected to an extra additional potential energy of the form $$V(t)=q^2t+q\dot qt^2$$ The Lagrange's equation of the oscillator due to the extra potential will contain:
- an extra term proportional to $t$
- an extra term proportional to $t^2$
- an extra term proportional to $(t+t^2)$
- no extra term
- The variational method in perturbation theory, when applied to obtain the value of the ground state energy:
- Always gives exact ground state energy
- gives energy value lower than the exact ground state energy
- gives energy value which is sometimes higher than or sometimes lower than the exact ground state energy
- gives energy value higher than or equal to the exact ground state energy
Friday, 2 December 2016
Problem set 34
- The second neighbour distance in a simple cubic system having lattice constant $a$ is:
- $\sqrt{2}a$
- $a$
- $\frac{\sqrt{3}}{2}a$
- $\sqrt{3}a$
- If the Debye characteristic frequency for copper is $6.55\times10^{12}Hz$, the Debye temperature for copper is :
- $200K$
- $314.5K$
- $405K$
- $150K$
- If the concentration of Schotty defects in a fcc crystal is 1 in $10^{10}$ at $300^oK$, the energy of formation in eV of Schottky defects will be
- 0.60
- 0.50
- 0.40
- 1.0
- Van der Waals attractive interaction between inert gas atoms varies with interatomic separation $(R)$ as :
- $-\frac{1}{R^2}$
- $-\frac{1}{R^3}$
- $-\frac{1}{R^6}$
- $-\frac{1}{R^{12}}$
- Metallic nickel crystallizes in fcc-type structure with lattice constant $a$. The interplanar distance between the diffracting planes (220) is this material is :
- $\frac{a}{2\sqrt{2}}$
- $\frac{a}{2}$
- $\frac{\sqrt{3}}{2}a$
- $\frac{a}{\sqrt{2}}$
Hence, answer is (A)