Problem set 17

1. If the perturbation $H' =ax$, where $a$ is a constant, is added to the infinite square well potential $$ \begin{align*} V(x) &= \begin{cases} 0 & \text{for } 0 \leq x \geq \pi \\ \infty & \text{otherwise} \end{cases} \end{align*} $$ The correction to the ground state energy, to first order in $a$, is
1. $\frac{a\pi}{2}$
2. $a\pi$
3. $\frac{a\pi}{4}$
4. $\frac{a\pi}{\sqrt{2}}$
Ground state wave function is given by $$\psi_0=\sqrt{\frac{2}{L}}\sin{\frac{n\pi x}{L}}=\sqrt{\frac{2}{\pi}}\sin{\frac{n\pi x}{\pi}}$$. Since, $L=\pi$. First order correction to energy is given by \begin{align*} E_0^{(1)}&=<\psi_0|H'|\psi_0>\\ &=\int_0^\pi\psi_0^*\:ax\:\psi_0\:dx\\ &={\scriptstyle \int_0^\pi\sqrt{\frac{2}{\pi}}\sin{\frac{n\pi x}{\pi}}\:ax\:\sqrt{\frac{2}{\pi}}\sin{nx}\:dx}\\ &=\frac{2a}{\pi}\int_0^\pi x\sin^2{nx}\:dx\\ &=\frac{2a}{\pi}\frac{1}{2}\int_0^\pi x(1-\cos{2nx})\:dx\\ &={\scriptstyle \frac{a}{\pi}\left\{\left[\frac{x^2}{2}\right]_0^\pi-\left[x\int \cos{2nx}\:dx\right.\right.}\\ &{\scriptstyle \left.\left.-\int\frac{dx}{dx}\left(\int\cos{2nx}\:dx\right)dx\right]_0^\pi\right\}}\\ &={\scriptstyle \frac{a}{\pi}\left\{\frac{\pi^2}{2}-\left[x\frac{sin{2nx}}{2n}+\frac{\cos{2nx}}{4n^2}\right]_0^\pi\right\}}\\ &=\frac{a}{2\pi} \end{align*}
2. Which of the following is an analytic function of the complex variable $z = x + iy$ in the domain $| z |< 2$?
1. $(3+x-iy)^7$
2. $(1+x+iy)^4(7-x-iy)^3$
3. $(1-2x-iy)^4(3-x-iy)^3$
4. $(x+iy-1)^{1/2}$
A function is analytic if it satisfies Cauchy–Riemann condition i.e. a function $f(z)$ is analytic if $\frac{\partial f(z)}{\partial\bar z}=0$ Above functions can be written in terms of $z$ using $z=x+iy$, $\bar z=x-iy$, $x=\frac{z+\bar z}{2}$ and $y=\frac{z-\bar z}{2i}$ \begin{align*} &(3+x-iy)^7=(3+\bar z)^7\\ &(1+x+iy)^4(7-x-iy)^4\\ &=(1+z)^4(7-z)^3\\ &(1-2x-iy)^4(3-x-iy)^3\\ &=\left(1-2\frac{z+\bar z}{2}-i\frac{z-\bar z}{2i}\right)^4(3-z)^3\\ &=\left(1-2z-\frac{\bar z}{2}\right)^4(3-z)^3\\ &(x+iy-1)^{1/2}=(z-1)^{1/2} \end{align*} For the functions which contain $\bar z$, $\frac{\partial f(z)}{\partial\bar z}\neq0$. Hence, the functions in the options (A) and (C) are not analytical.
For the functions which are functions of only $z$ have $\frac{\partial f(z)}{\partial\bar z}=0$. Hence, we have option either (B) or (C).
The option (B) i.e. $f(z)=(1+z)^4(7-z)^3$ is a polynomial in $z$ and polynomial in $z$ is analytic everywhere.
For the option (C) i.e. $f(z)=(z-1)^{1/2}$, $f'(z)=\frac{1}{2\sqrt{z-1}}$ and this function is analytic only for $|z|<1$. Our domain is $|z|<2$. Hence, it not analytical over the domain $|z|<2$.
Hence, the correct option is (B).
3. A particle in one dimension moves under the influence of a potential $V(x) = a x^6$, where $a$ is a real constant. For large $n$ the quantized energy level $E_n$ depends on $n$ as:
1. $E_n\sim n^3$
2. $E_n\sim n^{4/3}$
3. $E_n\sim n^{6/5}$
4. $E_n\sim n^{3/2}$
For large value of $n$, the semiclassical approximation is valid and for bound states we may use the Bohr-Sommerfeld quantization condition: $$n\hbar=\oint p\:dq$$ The total energy of system is $E=\frac{p^2}{2m}+ax^6$, hence $$p=\sqrt{2m(E-ax^6)}$$ $$\oint p\:dq=\int_{x_a}^{x_b}\sqrt{2m(E-ax^6)}dx$$ Where $x_a$ and $x_b$ are classical turning points. Turning point is the point at which $E=V(x)$, hence we get, $$E=ax^6$$ Above equation is true for $x=\pm\left(\frac{E}{a}\right)^{1/6}$ $$\oint p\:dq=\int_{-\left(\frac{E}{a}\right)^{1/6}}^{\left(\frac{E}{a}\right)^{1/6}}\sqrt{2m(E-ax^6)}dx$$ Let us scale the integration with substitution $x=\left(\frac{E}{a}\right)^{1/6}$ \begin{align*} &\oint p\:dq\\ &=\sqrt{2m}\left(\frac{E}{a}\right)^{2/3}\int_{-1}^1\sqrt{1-y^6)}dy\\ &=n\hbar \end{align*} Hence, $E_n\sim n^{3/2}$
4. A resistance is measured by passing a current through it and measuring the resulting voltage drop. If the voltmeter and the ammeter have uncertainties of 3% and 4%, respectively, then
1. The uncertainty in the value of the resistance is
1. 7.0%
2. 3.5%
3. 5.0%
4. 12.0%
2. The uncertainty in the computed value of the power dissipated in the resistance is
1. 7%
2. 5%
3. 11%
4. 9%

If $\Delta x$ and $\Delta y$ are uncertainties in measurements of $x$ and $y$, then uncertainty in $z$ i.e. $\Delta z$, for different cases is given by \begin{eqnarray} \begin{array}{cc} {\scriptstyle z=x\pm y }&{\scriptstyle\Delta z=\sqrt{(\Delta x)^2+(\Delta y)^2}}\\ {\scriptstyle z=xy} &{\scriptstyle\Delta z=|xy|\sqrt{\left(\frac{\Delta x}{x}\right)^2+\left(\frac{\Delta y}{y}\right)^2}}\\ {\scriptstyle z=\frac{x}{y}} &{\scriptstyle\Delta z=\left|\frac{x}{y}\right|\sqrt{\left(\frac{\Delta x}{x}\right)^2+\left(\frac{\Delta y}{y}\right)^2}}\\ {\scriptstyle z=x^n} &{\scriptstyle\Delta z=\left|n\right|x^{n-1}\Delta x}\\ {\scriptstyle z=f(x,y)} &{\scriptstyle \Delta z=\sqrt{\left(\frac{\partial f}{\partial x}\right)^2(\Delta x)^2+\left(\frac{\partial f}{\partial y}\right)^2(\Delta y)^2}}\\ \end{array} \end{eqnarray} In our case $\Delta V=3\%$ and $\Delta I=4\%$, as $R=\frac{V}{I}$ \begin{align*} \Delta R&=\left|\frac{V}{I}\right|\sqrt{\left(\frac{\Delta V}{V}\right)^2+\left(\frac{\Delta I}{I}\right)^2}\\ &=\left|\frac{100}{100}\right|\sqrt{\left(\frac{3}{100}\right)^2+\left(\frac{4}{100}\right)^2}\\ &=\frac{5}{100}\\ \Delta R&=5\% \end{align*} Similarly, using $P=VI$, $\Delta P=5\%$. Hence, anwers are (C) and (B).

Problem set 16

1. Consider the digital circuit shown below in which the input $C$ is always high (1).
   
   The truth table for the circuit can be written as

   A	B	Z
   0	0
   0	1
   1	0
   1	1

   The entries in the Z column (vertically) are
1. 1010
2. 0100
3. 1111
4. 1011
AND gate has output high when both inputs are high, OR gate has output high when any one or both inputs high and EXOR gate has high output when any one input is high but not both inputs hight. Hence, answer is (D)
2. Let $p_n(x)$ (where $n = 0,1,2,\dots$) be a polynomial of degree $n$ with real coefficients, defined in the interval $2\leq n\leq 4$. If $\int_2^4p_n(x)p_m(x)dx=\delta_{nm}$, then
1. $p_0(x)=\frac{1}{\sqrt{2}}$ and $p_1(x)=\sqrt{\frac{3}{2}}(-3-x)$
2. $p_0(x)=\frac{1}{\sqrt{2}}$ and $p_1(x)=\sqrt{3}(3+x)$
3. $p_0(x)=\frac{1}{2}$ and $p_1(x)=\sqrt{\frac{3}{2}}(3-x)$
4. $p_0(x)=\frac{1}{\sqrt{2}}$ and $p_1(x)=\sqrt{\frac{3}{2}}(3-x)$
For $p_0(x)=\frac{1}{\sqrt{2}}$, we have \begin{align*} \int_2^4p_0(x)p_0(x)dx&=\frac{1}{2}\int_2^4dx\\ &=\frac{1}{2}[x]_2^4=1 \end{align*} Hence, $p_0(x)=\frac{1}{\sqrt{2}}$ is correct option. For, $p_1(x)=\sqrt{\frac{3}{2}}(3-x)$, we have \begin{align*} &\int_2^4p_1(x)p_1(x)dx\\ &=\frac{3}{2}\int_2^4(3-x)^2dx\\ &=\frac{3}{2}\int_2^4(9-6x+x^2)dx \end{align*} \begin{align*} &\int_2^4p_1(x)p_1(x)dx\\ &=\frac{3}{2}\left[9x-3x^2+\frac{x^3}{3}\right]_2^4\\ &=1 \end{align*} \begin{align*} &\int_2^4p_0(x)p_1(x)dx\\ &=\sqrt{\frac{3}{4}}\int_2^4(3-x)dx\\ &=\sqrt{\frac{3}{4}}\left[3x-\frac{x^2}{2}\right]_2^4\\ &=0 \end{align*} Hence, orthonormality condition is satified for $p_0(x)=\frac{1}{\sqrt{2}}$ and $p_1(x)=\sqrt{\frac{3}{2}}(3-x)$. Hence, answer is (D)
3. The energy levels of the non-relativistic electron in a hydrogen atom (i.e. in a Coulomb potential $V(r)\propto -1/r$) are given by $E_{nlm}\propto -1/n^2$, where $n$ is the principal quantum number, and the corresponding wave functions are given by $\psi_{nlm}$, where $l$ is the orbital angular momentum quantum number and $m$ is the magnetic quantum number. The spin of the electron is not considered. Which of the following is a correct statement?
1. There are exactly $( 2l+1)$ different wave functions $\psi_{nlm}$, for each $E_{nlm}$.
2. There are $l(l+1)$ different wave functions $\psi_{nlm}$, for each $E_{nlm}$.
3. $E_{nlm}$ does not depend on $l$ and $m$ for the Coulomb potential.
4. There is a unique wave function $\psi_{nlm}$ for each $E_{nlm}$.
(C) $E_{nlm}$ does not depend on $l$ and $m$ for the Coulomb potential.
4. The Hamiltonian of an electron in a constant magnetic field $\vec B$ is given by $H=\mu \vec\sigma\cdot\vec B$ where $\mu$ is a positive constant and $\vec\sigma= (\sigma_1, \sigma_2, \sigma_3 )$ denotes the Pauli matrices. Let $\omega = \mu B/\hbar$ and $I$ be the $2\times2$ unit matrix. Then the operator $e^{iHt/\hbar}$ simplifies to
1. $I\cos{\frac{\omega t}{2}}+\frac{i\vec\sigma\cdot\vec B}{B}\sin{\frac{\omega t}{2}}$
2. $I\cos{\omega t}+\frac{i\vec\sigma\cdot\vec B}{B}\sin{\omega t}$
3. $I\sin{\omega t}+\frac{i\vec\sigma\cdot\vec B}{B}\cos{\omega t}$
4. $I\sin{2\omega t}+\frac{i\vec\sigma\cdot\vec B}{B}\cos{2\omega t}$
$$H=\mu\vec\sigma\cdot\vec B=\mu B\vec\sigma\cdot\hat n$$ where $\hat n$ is unit vecot along $\vec B$. Using $\omega=\mu B/\hbar$, we get $$H=\hbar\omega\vec\sigma\cdot\hat n$$ $$\therefore e^{iHt/\hbar}=e^{i\omega t(\vec\sigma\cdot\hat n)}$$ \begin{align*} e^{i\omega t(\vec\sigma\cdot\hat n)}&=1+i\omega t(\vec\sigma\cdot\hat n)\\ &+\frac{(i\omega t)^2}{2!}(\vec\sigma\cdot\hat n)^2\\ &+\frac{(i\omega t)^3}{3!}(\vec\sigma\cdot\hat n)^3\\ &+\frac{(i\omega t)^4}{4!}(\vec\sigma\cdot\hat n)^4\\ &+\dots\quad (1) \end{align*} But, \begin{align*} (\vec\sigma\cdot\hat n)&=\sigma_xn_x+\sigma_yn_y+\sigma_zn_z\\ &=\begin{pmatrix}0&n_x\\n_x&0\end{pmatrix}+ \begin{pmatrix}0&-n_y\\in_y&0\end{pmatrix}\\ &+\begin{pmatrix}n_z&0\\0&-n_z\end{pmatrix} \end{align*} $$(\vec\sigma\cdot\hat n)=\begin{pmatrix}n_z&n_x-n_y\\n_x+in_y&-n_z\end{pmatrix}$$ It can be verified that $(\vec\sigma\cdot\hat n)^2=I$. Hence, equation (1) becomes \begin{align*} e^{i\omega t(\vec\sigma\cdot\hat n)}&=\\ &I+i\omega t(\vec\sigma\cdot\hat n)\\ &-\frac{(\omega t)^2}{2!}I\\ &-i\frac{(\omega t)^3}{3!}(\vec\sigma\cdot\hat n)\\ &+\frac{(\omega t)^4}{4!}I-\dots \end{align*} \begin{align*} e^{i\omega t(\vec\sigma\cdot\hat n)}&=I\left[1-\frac{(\omega t)^2}{2!}+\frac{(\omega t)^4}{4!}-..\right]\\ &+(\vec\sigma\cdot\hat n)\left[\omega t-\frac{(\omega t)^3}{3!}+\dots\right] \end{align*} $$e^{i\omega t(\vec\sigma\cdot\hat n)}=I\cos{\omega t}+\frac{\vec\sigma\cdot\vec B}{B}\sin{\omega t}$$
5. The Hamiltonian of a system with $n$ degrees of freedom is given by $H(q_1, \dots,q_n;p_1,\dots,p_n;t)$, with an explicit dependence on the time $t$ . Which of the following is correct?
1. Different phase trajectories cannot intersect each other.
2. $H$ always represents the total energy of the system and is a constant of the motion.
3. The equations $\dot q_i =\partial H/\partial p_i$, $\dot p_i =-\partial H/\partial q_i$ are not valid since $H$ has explicit time dependence.
4. Any initial volume element in phase space remains unchanged in magnitude under time evolution.
If $H$ depends explicitly on time, then phase trajectories can intersect. A constant Hamiltonian is the total energy if the potential is velocity independent. The equations $\dot q_i =\partial H/\partial p_i$, $\dot p_i =-\partial H/\partial q_i$ are are always valid. The fourth option, Any initial volume element in phase space remains unchanged in magnitude under time evolution, is a Liouville theorem. Hence, answer is (D).

Problem set 15

1. For constant uniform electric and magnetic fields $\vec E=\vec E_0$ and $\vec B=\vec B_0$,it is possible to choose a gauge such that the scalar potential $\phi$ and vector potential $\vec A$ are given by
   1. $\phi=0$ and $\vec A=\frac{1}{2}\left(\vec B_0\times\vec r\right)$
   2. $\phi=-\vec E\cdot \vec r$ and $\vec A=\frac{1}{2}\left(\vec B_0\times\vec r\right)$
   3. $\phi=-\vec E\cdot \vec r$ and $\vec A=0$
   4. $\phi=0$ and $\vec A=-\vec E t$
   Electric field $\vec E$ and magnetic field $\vec B$ are related to vector and scalar potentials by $$\vec B=\vec\nabla\times\vec A\quad (1)$$ $$\vec E=-\vec\nabla\phi-\frac{\partial\vec A}{\partial t}\quad (2)$$ Substituting values $\phi=-\vec E\cdot \vec r$ and $\vec A=\frac{1}{2}\left(\vec B_0\times\vec r\right)$ in equations (1) and (2), we get $\vec E=\vec E_0$ and $\vec B=\vec B_0$ (Verify this). Hence answer is (B)$\phi=-\vec E\cdot \vec r$ and $\vec A=\frac{1}{2}\left(\vec B_0\times\vec r\right)$.
2. Let $\vec{a}$ and $\vec{b}$ be two distinct three-dimensional vectors. Then the component of $\vec{b}$ that is perpendicular to $\vec{a}$ is given by
1. $\frac{\vec{a}\times(\vec{b}\times\vec{a})}{a^2}$
2. $\frac{\vec{b}\times(\vec{b}\times\vec{a})}{b^2}$
3. $\frac{(\vec{a}.\vec{b})\vec{b}}{b^2}$
4. $\frac{(\vec{b}.\vec{a})\vec{a}}{a^2}$
\begin{align*} \frac{\vec{a}\times(\vec{b}\times\vec{a})}{a^2}&=\frac{(\vec{a}\cdot\vec{a})\vec{b}-(\vec{a}\cdot\vec{b})\vec{a}}{a^2}\\ &=\frac{a^2\vec{b}-ab\cos\theta\vec{a}}{a^2} \end{align*} \begin{align*} & \vec{a}\cdot\frac{\vec{a}\times(\vec{b}\times\vec{a})}{a^2}\\ &=\frac{a^2\vec{a}\cdot\vec{b}-ab\cos\theta\vec{a}\cdot\vec{a}}{a^2}\\ &=\frac{a^3b\cos\theta-a^3b\cos\theta}{a^2}\\ &=0 \end{align*} Hence answer is (A)
3. The wavefunction of a particle is given by $\psi=\left(\frac{1}{\sqrt{2}}\phi_0+i\phi_1\right)$, where $\phi_0$ and $\phi_1$ are the normalized eigenfunctions with energies $E_0$ and $E_1$ corresponding to the ground state and first excited state, respectively. The expectation value of the Hamiltonian in the state $\psi$ is
   1. $\frac{E_0}{2}+E_1$
   2. $\frac{E_0}{2}-E_1$
   3. $\frac{E_0-2E_1}{3}$
   4. $\frac{E_0+2E_1}{3}$
   $H\phi_0=E_0\phi_0$ and $H\phi_1=E_1\phi_1$ \begin{align*} \left< H \right>=\frac{\left< \psi |H|\psi \right>}{\left< \psi |\psi \right>} \end{align*} \begin{align*} &<\psi|H|\psi>=\\ &\left<\left.\frac{1}{\sqrt{2}}\phi_0+i\phi_1\right|H\left|\frac{1}{\sqrt{2}}\phi_0+i\phi_1\right.\right> \end{align*} \begin{align*} &<\psi|H|\psi>=\\ &\left<\left.\frac{1}{\sqrt{2}}\phi_0+i\phi_1\right|\frac{1}{\sqrt{2}}E_0\phi_0+iE_1\phi_1 \right> \end{align*} \begin{align*} &<\psi|H|\psi>=\\ &\frac{1}{2}E_0\left<\left.\phi_0\right|\phi_0\right>+E_1(i)(-i) \left<\left.\phi_1\right|\phi_1 \right> \end{align*} Using orthonormality condition $$<\psi|H|\psi>=\frac{1}{2}E_0+E_1$$ \begin{align*} <\psi|\psi>&=\\ &\left<\left.\frac{1}{\sqrt{2}}\phi_0+i\phi_1\right|\frac{1}{\sqrt{2}}\phi_0+i\phi_1\right> \end{align*} \begin{align*} <\psi|\psi>&=\\ &\frac{1}{2}\left<\left.\phi_0\right|\phi_0\right>+(-i)(i)\left<\left.\phi_1\right|\phi_1\right> \end{align*} $$<\psi|\psi>=\frac{1}{2}+1=\frac{3}{2}$$ \begin{align*} \left< H \right> &=\frac{\frac{1}{2}E_0+E_1}{\frac{3}{2}}\\ &=\frac{E_0+2E_1}{3} \end{align*} Hence, answer is (D)
4. Which of the following matrices is an element of the group SU(2)
1. $\begin{pmatrix}1&1\\0&1\end{pmatrix}$
2. $\begin{pmatrix}\frac{1+i}{\sqrt{3}}&\frac{-1}{\sqrt{3}}\\\frac{1}{\sqrt{3}}&\frac{1-i}{\sqrt{3}}\end{pmatrix}$
3. $\begin{pmatrix}2+i&i\\3&1+i\end{pmatrix}$
4. $\begin{pmatrix}\frac{1}{2}&\frac{\sqrt{3}}{2}\\\frac{\sqrt{3}}{2}&\frac{1}{2}\end{pmatrix}$
The special unitary group of degree $n$, denoted $SU(n)$, is the Lie group of $n×n$ unitary matrices with determinant 1. For $2\times2$ matrix the group is denoted by $SU(2)$. Let $U=\begin{pmatrix}a&b\\c&d\end{pmatrix}$. As $U$ is unitary, we have $UU^\dagger=U^\dagger U=1$. This gives $$aa^*+bb^*=1\quad(1)$$ $$cc^*+dd^*=1\quad(2)$$ $$ac^*+bd^*=0\quad(3)$$ $$ca^*+db^*=0\quad(4)$$ Also $$det~U=ad-bc=1\quad(5)$$ From (4), we have $$\frac{d}{c}=-\frac{a^*}{b^*}$$ substituting in (5) $$-(aa^*+bb^*)\frac{c}{b^*}=1$$ Using (1) we get $$c=-b^*$$ Similarly, we can show that $$d=a^*$$ Hence, in general the $2\times2$ matrix $U=\begin{pmatrix}a&b\\c&d\end{pmatrix}$ is of $SU(2)$ group if
• Its determinant is 1 and
• It is in the form $U=\begin{pmatrix}a&b\\-b^*&a^*\end{pmatrix}$
These conditions are satisfied by $\begin{pmatrix}\frac{1+i}{\sqrt{3}}&\frac{-1}{\sqrt{3}}\\\frac{1}{\sqrt{3}}&\frac{1-i}{\sqrt{3}}\end{pmatrix}$. Hence answer is (B).
5. The acceleration due to gravity $(g)$ on the surface of Earth is approximately 2.6 times that on the surface of Mars. Given that the radius of Mars is about one half the radius of Earth, the ratio of the escape velocity on Earth to that on Mars is approximately
1. 1.1
2. 1.3
3. 2.3
4. 5.2
Escape velocity is given by $$v=\sqrt{\frac{2GM}{R}}$$ On earth's surface force acting on body is $F=mg$, hence $g=\frac{F}{m}$. However, $F=\frac{GM_Em}{R_E^2}$, hence $g=\frac{\frac{GM_Em}{R_E^2}}{m}$, hence $GM=R_E^2g$ $$v_e=\sqrt{2R_Eg}$$ $$\frac{v_E}{v_M}=\sqrt{\frac{2R_Eg_E}{2R_Mg_M}}=\sqrt{5.2}=2.3$$ Hence, answer is (C)

Problem set 14

1. A particle of unit mass moves in a potential $V(x)=ax^2+\frac{b}{x^2}$, where $a$ and $b$ are positive constants. The angular frequency of small oscillations about the minimum of the potential is
1. $\sqrt{8b}$
2. $\sqrt{8a}$
3. $\sqrt{8a/b}$
4. $\sqrt{8b/a}$
The equation of motion is $$m\ddot{x}=F=-kx$$ $$\ddot{x}=-\frac{k}{m}x=-\omega^2 x$$ \begin{align*} \omega&=\sqrt{-\frac{\ddot{x}}{x}}=\sqrt{-\frac{m\ddot{x}}{mx}}\\ &=\sqrt{-\frac{F}{mx}}=\sqrt{\frac{\frac{dV}{dx}}{mx}}\\ &=\sqrt{\frac{\frac{d^2V}{dx^2}}{m}} \end{align*} Minimum of potential occurs at mean position $x_0$. Hence frequency of oscillation about the minimum of the potential is $$\omega=\sqrt{\frac{\left.\frac{d^2V}{dx^2}\right|_{x=x_0}}{m}}$$ $$\frac{dV}{dx}=2ax-\frac{2b}{x^3}$$ At minimum potential energy, we have $$\left.\frac{dV}{dx}\right|_{x=x_0}=0$$ $$\therefore 2ax_0-\frac{2b}{x_0^3}=0$$ $$\therefore x_0^4=\frac{b}{a}$$ $$\frac{d^2V}{dx^2}=2a+\frac{6b}{x^4}$$ $$\left.\frac{d^2V}{dx^2}\right|_{x=x_0}=2a+\frac{6b}{x_0^4}=8a$$ $$\omega=\sqrt{\frac{\left.\frac{d^2V}{dx^2}\right|_{x=x_0}}{m}}=\sqrt{\frac{8a}{m}}=\sqrt{8a}$$
2. A signal of frequency 10 kHz is being digitized by an A/D converter. A possible sampling time which can be used is
1. $100\quad \mu s$
2. $40\quad \mu s$
3. $60\quad \mu s$
4. $200\quad \mu s$
The conversion time is the time required to complete a conversion of the input signal. It establishes the upper signal frequency limit that can be sampled without aliasing $$f_{max}=\frac{1}{2\times conversion~time}$$ \begin{align*} conversion~time &=\frac{1}{2\times f_{max}}\\ &=\frac{1}{2\times 10\times10^3}\\ &=5\times10^{-5}=50\mu S \end{align*} Hence answer is (B).
Supplementary information: AD converter specifications:
• The conversion time is the time required to complete a conversion of the input singnal. It establishes the upper signal frequency limit that can be sampled without aliasing $$f_{max}=\frac{1}{2\times conversion~time}$$
• Resolution: The number of bits in the converter gives the resolution $${\scriptstyle Resolution=\frac{full-scale~signal}{2^n}}$$
• Accuracy: Accuracy describes how close the measurement is to the actual value. $$Accuracy=\frac{V_{resolution}}{V_{signal}}\times 100\%$$
3. The electrostatic potential $V ( x, y)$ in free space in a region where the charge density $\rho$ is zero is given by $V ( x, y)=4e^{2x}+f(x)-3y$. Given that the x-component of the electric field, $E_x$, and $V$ are zero at the origin, $f (x)$ is
1. $3x^2-4e^{2x}+8x$
2. $3x^2-4e^{2x}+16x$
3. $4e^{2x}-8$
4. $3x^2-4e^{2x}$
$V ( x, y)$ is zero at origin is zero gives $f(0)=-4$. This requirement is satisfied by all options. So let us calculate electric field. $$\vec F=q_0\vec E$$ If test charge $q_0=1$ then \begin{align*} \vec E&=\vec F=-\vec \nabla V\\ &={\scriptstyle -\left(\hat i\frac{\partial}{\partial x}+\hat j\frac{\partial}{\partial y}+\hat k\frac{\partial}{\partial z}\right)\left(4e^{2x}+f(x)-3y\right)} \end{align*} $$\vec E=-\hat i \left(8e^{2x}+\frac{\partial f(x)}{\partial x}\right)+\hat j(3)$$ Hence, x-component of electric field is $$E_x(x)=-\left(8e^{2x}+\frac{\partial f(x)}{\partial x}\right)$$ However, $E_x=0$ at origin. $$E_x(0)=-\left(8e^{0}+\frac{\partial f(0)}{\partial x}\right)=0$$ Hence, $$\frac{\partial f(0)}{\partial x}=-8$$ For $f(x)=3x^2-4e^{2x}+8x$, $$\frac{\partial f}{\partial x}=6x-8e^{2x}+8$$ $$\frac{\partial f(0)}{\partial x}=0-8+8=0$$
For $f(x)=3x^2-4e^{2x}+16x$, $$\frac{\partial f}{\partial x}=6x-8e^{2x}+16$$ $$\frac{\partial f(0)}{\partial x}=0-8+16=8$$
For $f(x)=4e^{2x}-8$, $$\frac{\partial f}{\partial x}=8e^{2x}$$ $$\frac{\partial f(0)}{\partial x}=8$$
For $f(x)=3x^2-4e^{2x}$, $$\frac{\partial f}{\partial x}=6x-8e^{2x}$$ $$\frac{\partial f(0)}{\partial x}=0-8=-8$$ Hence, Answer is (D).
4. Consider the transition of liquid water to steam as water boils at a temperature of $100^oC$ under a pressure of 1 atmosphere. Which one of the following quantities does not change discontinuously at the transition?
1. The Gibbs free energy
2. The internal energy
3. The entropy
4. The specific volume
(A) The Gibbs free energy.
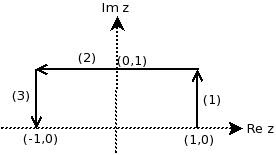
5. The value of the integral $\int\limits_Cdz\:z^2\:e^z$, where C is an open contour in the complex z-plane as shown in the figure below, is:
   
   1. $\frac{5}{e}+e$
   2. $e-\frac{5}{e}$
   3. $\frac{5}{e}-e$
   4. $-\frac{5}{e}-e$
   \begin{align*} &\int_Cdz\:z^2\:e^z\\ &=\int_Cd(x+iy)\:(x+iy)^2\:e^{(x+iy)} \end{align*} Along path (1) $x=1$, $dx=0$ and $y$ changes 0 to 1 \begin{align*} I_1&=i\int_0^1 (1+iy)^2e^{(1+iy)}dy\\ &=i\int_0^1 (1-y^2+2iy)e^{(1+iy)}dy \end{align*} Along path (2) $y=1$, $dy=0$ and $x$ changes 1 to $-1$ \begin{align*} I_2&=\int_{-1}^1 (x+i)^2e^{(x+i)}dx\\ &=\int_{-1}^1 (x^2-1+2ix)e^{(x+i)}dx \end{align*} Along path (3) $x=-1$, $dx=0$ and $y$ changes 1 to 0 \begin{align*} I_3&=i\int_{-1}^0 (-1+iy)^2e^{(-1+iy)}dy\\ &=i\int_{-1}^0 (1-y^2-2iy)e^{(-1+iy)}dy \end{align*} $$I=I_1+I_2+I_3=\frac{5}{e}+e$$

Problem set 13

1. A rod of length $l_0$ makes an angle $\theta_0$ with the y-axis in its rest frame, while the rest frame moves to the right along the x-axis with relativistic speed $v$ with respect to lab frame. If $\gamma=\frac{1}{\sqrt{1-v^2/c^2}}$, the angle $\theta$ in the lab frame is
1. $\theta=\tan^{-1}{(\gamma\tan\theta_0)}$
2. $\theta=\tan^{-1}{(\gamma\cot\theta_0)}$
3. $\theta=\tan^{-1}{(\frac{1}{\gamma}\tan\theta_0)}$
4. $\theta=\tan^{-1}{(\frac{1}{\gamma}\cot\theta_0)}$

The x and y components of length $l_0$ are given by $l_x=l_0\sin\theta_0$, $l_y=l_0\cos\theta_0$ As the frame is moving along x-axis to the right, there is contraction of length in $l_x$ only $$l_x'=(l_0\sin\theta_0)\sqrt{1-v^2/c^2}$$ $$l_y'=l_0\cos\theta_0$$ \begin{align*} \tan\theta&=\frac{l_y'}{l_x'}\\ &=\frac{l_0\cos\theta_0}{(l_0\sin\theta_0)\sqrt{1-v^2/c^2}}\\ &=\gamma\cot\theta_0 \end{align*} $$\theta=\tan^{-1}(\gamma\cot\theta_0)$$
2. A particle of mass $m$ moves in a potential $V(x)=\frac{1}{2}m\omega^2x^2+\frac{1}{2}m\mu v^2$, where $x$ is the position coordinate, $v$ is the speed, and $\omega$ and $\mu$ are constants. The canonical (conjugate) momentum of the particle is
1. $p=m(1+\mu)v$
2. $p=mv$
3. $p=m\mu v$
4. $p=m(1-\mu)v$
\begin{align*} L&=T-V(x)\\ &=\frac{1}{2}m\dot x^2-\frac{1}{2}m\omega^2x^2-\frac{1}{2}m\mu \dot v^2\\ &=\frac{1}{2}m\dot x^2-\frac{1}{2}m\omega^2x^2-\frac{1}{2}m\mu \dot x^2 \end{align*} Conjugate momentum is given by \begin{align*} p&=\frac{\partial L}{\partial\dot x}\\ &=m\dot x-m\mu\dot x=m(1-\mu)v \end{align*}
3. A solid sphere of radius $R$ carries a uniform volume charge density $\rho$. The magnitude of electric field inside the sphere at a distance $r$ from center is
1. $\frac{r\rho}{3\epsilon_0}$
2. $\frac{R\rho}{3\epsilon_0}$
3. $\frac{R^2\rho}{r\epsilon_0}$
4. $\frac{R^3\rho}{r^2\epsilon_0}$
According to Gauss law , if the surface encloses a charge $q$ within it, then net flux through the surface is $q/\epsilon_0$. The flux is given by $$\phi_E=\int_S\vec E.d\vec A=\frac{q}{\epsilon_0}$$ If $\rho$ is the volume charge density, the charge enclosed within a distance $r$ is $q=\frac{4}{3}\pi r^3\rho$ and $$\int_S\vec E.d\vec A=E(4\pi r^2)$$ $$E(4\pi r^2)=\frac{4}{3\epsilon_0}\pi r^3\rho$$ $$E=\frac{\rho r}{3\epsilon_0}$$
4. The electric field $\vec E(\vec r,t)$ for a circularly polarized electromagnetic wave propagating along the positive $z$ direction is
   1. $E_0(\hat x+\hat y)exp[i(kz-\omega t)]$
   2. $E_0(\hat x+i\hat y)exp[i(kz-\omega t)]$
   3. $E_0(\hat x+i\hat y)exp[i(kz+\omega t)]$
   4. $E_0(\hat x+\hat y)exp[i(kz+\omega t)]$
   Plane wave travelling along the positive z-axis is given by $$\vec E(z,t)=\vec E_0 cos(kz-\omega t)$$ Plane wave travelling along the negative z-axis is given by $$\vec E(z,t)=\vec E_0 cos(kz+\omega t)$$ A beam linearly polarized along the x-axis and traveling in the positive z-direction can be represented by:$$\vec E(z,t)= E_0 cos(kz-\omega t)\hat x$$ Circularly polarized light can be represented by the expressions: \begin{align*} \vec E_{RCP}(z,t)&= E_0 \left(cos(kz-\omega t)\hat x\right.\\ &{}\left.+sin(kz-\omega t)\hat y\right) \end{align*} \begin{align*} \vec E_{LCP}(z,t)&= E_0 \left(cos(kz-\omega t)\hat x\right.\\ &\left.-sin(kz-\omega t)\hat y\right) \end{align*} Consider option (A) \begin{align*} \vec E&=E_0(\hat x+\hat y)exp[i(kz-\omega t)]\\ &=E_0(\hat x+\hat y)\left(cos(kz-\omega t)\right.\\ &{}\left.+isin(kz-\omega t)\right)\\ &=E_0\left[cos(kz-\omega t) \hat x\right.\\ &\left.{}+cos(kz-\omega t)\hat y\right]\\ &{}+iE_0\left[sin(kz-\omega t)\hat x\right.\\ &{}\left.+sin(kz-\omega t)\hat y\right] \end{align*} Hence real part of $\vec E$ is \begin{align*} Re \vec E&=E_0\left[cos(kz-\omega t) \hat x\right.\\ &{}\left.+cos(kz-\omega t)\hat y\right] \end{align*} which represents plane polarized light.
   Now consider the option (B) \begin{align*} \vec E&=E_0(\hat x+i\hat y)exp[i(kz-\omega t)]\\ &=E_0(\hat x+i\hat y)\left(cos(kz-\omega t)\right.\\ &\left. +isin(kz-\omega t)\right)\\ &=E_0\left[cos(kz-\omega t) \hat x\right.\\ &\left.-sin(kz-\omega t)\hat y\right]\\ &+iE_0\left[sin(kz-\omega t)\hat x\right.\\ &\left.+cos(kz-\omega t)\hat y\right] \end{align*} \begin{align*} Re \vec E&=E_0\left[cos(kz-\omega t) \hat x\right.\\ &\left.-sin(kz-\omega t)\hat y\right] \end{align*} Which represents a circularly polarized light, as \begin{align*} E_x^2+E_y^2&=E_0^2cos^2(kz-\omega t)\\ &+E_0^2sin^2(kz-\omega t)\\ &=E_0^2 \end{align*} is equation of circle. Hence (B) is correct option.
5. An unbiased coin is tossed $n$ times. The probability that exactly $m$ heads will come up is
1. $\frac{n}{2^m}$
2. $\frac{1}{2^n}\frac{n!}{m!(n-m)!}$
3. $\frac{1}{2^m}\frac{n!}{m!(n-m)!}$
4. $\frac{m}{2^n}$
This problem is equivalent to 1D random walk problem. In a single toss probability getting head is $p=\frac{1}{2}$ and probability of getting tail is $q=\frac{1}{2}$. In a sequences of $n$ tosses probability of getting $m$ heads and $n-m$ tails is given by $$p^mq^{(n-m)}=\left(\frac{1}{2}\right)^m\left(\frac{1}{2}\right)^{n-m}$$ However, total combinations of $m$ times head up and $(n-m)$ times tail up are given by $$\frac{n!}{m!(n-m)!}$$ Hence, probability of getting $m$ heads is \begin{align*} P&=\frac{n!}{m!(n-m)!}\left(\frac{1}{2}\right)^m\left(\frac{1}{2}\right)^{n-m}\\ &=\frac{n!}{m!(n-m)!}\left(\frac{1}{2}\right)^n \end{align*} Hence, answer is (B).

Problem set 12

1. A plane wave of electric and magnetic fields $\vec E_0$ , $\vec B_0$ and frequency $\omega$ enters in a conducting bar of conductivity $\sigma$ along z-axis. Which of the following pairs of equations best represents the propagating wave? ($k\longrightarrow $ wave number)
1. $\vec E(z,t)=E_0e^{-ikz}e^{i(kz-\omega t)}\hat x$ and $\vec B(z,t)=\frac{k}{\omega} E_0e^{-ikz}e^{i(kz-\omega t+\phi)}\hat y$
2. $\vec E(z,t)=E_0e^{-kz}e^{i(kz-\omega t)}\hat x$ and $\vec B(z,t)=\frac{k}{\omega} E_0e^{-kz}e^{i(kz-\omega t+\phi)}\hat y$
3. $\vec E(z,t)=\frac{k}{\omega}E_0e^{-kz}e^{i(kz-\omega t)}\hat x$ and $\vec B(z,t)=\frac{k}{\omega} E_0e^{-ikz}e^{i(kz-\omega t+\phi)}\hat y$
4. $\vec E(z,t)=\frac{k}{\omega}E_0e^{-kz}e^{i(kz-\omega t)}\hat x$ and $\vec B(z,t)= E_0e^{-kz}e^{i(kz-\omega t+\phi)}\hat y$
In electromagnetic wave the electric and magnetic fields and propagation direction are mutually perpendicular to each other. Hence as wave travels in z-direction, electric and magnetic fields must be in x and y-directions. Let electric field is in x-direction. The wave equation for electric field in electromagnetic wave is given by $$\vec E(z,t)=E_0e^{-kz}e^{i(kz-\omega t)}\hat x$$ The term $e^{i(kz-\omega t)}$ is a plane equation and the term $e^{-kz}$ gives exponential decay of wave.
Magnetic field in plane electromagnetic wave in a conducting medium is related to the electric field by \begin{align*} \vec B&=\frac{\vec k}{\omega}\times\vec E\\ &=\frac{k}{\omega}\left|\vec E\right|\hat z\times\hat x\\ &=\frac{k}{\omega}\left|\vec E\right|\hat y\\ &=\frac{k}{\omega}E_0e^{-kz}e^{i(kz-\omega t)}\hat y \end{align*} Also in conducting media there is a phase difference of $\phi$ between $\vec E$ and $\vec B$ $$\therefore\vec B=\frac{k}{\omega}E_0e^{-kz}e^{i(kz-\omega t+\phi)}\hat y$$
2. A plane electromagnetic wave travelling in vacuum is incident normally on a non-magnetic, non-absorbing medium of refractive index $n$. The incident $(E_i)$, reflected $(E_r)$ and transmitted $(E_t)$, electric fields are given as $E_i=E_{0i}exp[i(kz-\omega t)]$, $E_r=E_{0r}exp[i(k_rz-\omega t)]$, $E_t=E_{0t}exp[i(k_tz-\omega t)]$. If $E_{0i}=2 V/m$ and $n=1.5$ then the application of appropriate boundary conditions leads to
1. $E_{0r}=-\frac{3}{5} V/m$, $E_{0t}=\frac{7}{5} V/m$
2. $E_{0r}=-\frac{1}{5} V/m$, $E_{0t}=\frac{9}{5} V/m$
3. $E_{0r}=-\frac{2}{5} V/m$, $E_{0t}=\frac{8}{5} V/m$
4. $E_{0r}=\frac{4}{5} V/m$, $E_{0t}=\frac{6}{5} V/m$
Wave is travelling in vacuum, hence $n_1=1$, for the medium $n_2=1.5$. \begin{align*} E_{0r}&=\frac{n_1-n_2}{n_1+n_2}E_{0i}\\ &=\frac{1-1.5}{1+1.5}\times 2\\ &=-\frac{1}{2.5}=-\frac{2}{5} \end{align*} \begin{align*} E_{0t}&=\frac{2n_1}{n_1+n_2}E_{0i}\\ &=\frac{2}{1.5+1}\times 2\\ &=\frac{4}{2.5}=\frac{8}{5} \end{align*}
3. The magnetic field due to the $TE_{11}$ mode in a rectangular wave guide aligned along Z-axis is given by $H_z=H_1\cos{(0.5\:\pi x)}\cos{(0.6\:\pi y)}$, where $x$ and $y$ are in cm. Then dimensions of the rectangular wave guide $a$ and $b$, respectively, are
1. 2.00 cm and 1.66 cm
2. 1.66 cm and 2.66 cm
3. 2.54 cm and 1.66 cm
4. 1.66 cm and 1.25 cm
In a rectangular wave guide the longitudinal magnetic field is given by $$H_z(x,y)=H_0\cos{(k_xx)}\cos{(k_yy)}$$ where $k_x=\frac{n\pi}{a}$ and $k_y=\frac{m\pi}{b}$. For $TE_{11}$ mode $n=m=1$.
Hence, $k_x=\frac{\pi}{a}$ and $k_y=\frac{\pi}{b}$
Hence, $a=\frac{\pi}{k_x}=\frac{1}{0.5}=2$ cm and $b=\frac{\pi}{k_y}=\frac{1}{0.6}=1.66$ cm
Hence, answer is (A) 2.00 cm and 1.66 cm.
4. The Boolean expression $B\cdot(A+B)+A\cdot(\bar B+A)$ can be realized using minimum number of
1. 1 AND gate
2. 2 AND gates
3. 1 OR gate
4. 2 OR gates
\begin{align*} {}&{}B\cdot(A+B)+A\cdot(\bar B+A)\\ &=B\cdot A+B\cdot B+A\cdot\bar B+A\cdot A \end{align*} But $ B\cdot B=B$ and $ A\cdot A=A$ \begin{align*} {}&{}B\cdot(A+B)+A\cdot(\bar B+A)\\ &=B\cdot A+B+A\cdot\bar B+A\\ &=B\cdot(A+1)+A\cdot(\bar B+1) \end{align*} But $A+1=1$ and $(\bar B+1)=1$ $$B\cdot(A+B)+A\cdot(\bar B+A)=B+A$$ Hence answer is (C) 1 OR gate
5. For a diatomic molecule with the vibrational quantum number $n$ and rotational quantum number $J$, the vibrational level spacing $\Delta E_n=E_n-E_{n-1}$ and the rotational level spacing $\Delta E_J=E_J-E_{J-1}$ are approximately
1. $\Delta E_n=$ constant, $\Delta E_J=$ constant
2. $\Delta E_n=$ constant, $\Delta E_J\propto J$
3. $\Delta E_n\propto n$, $\Delta E_J\propto J$
4. $\Delta E_n\propto n$, $\Delta E_J\propto J^2$
(B)$\Delta E_n=$ constant, $\Delta E_J\propto J$

Problem set 11

1. An electron with rest mass $m_0$ is accelerated. Its relativistic mass is $2m_0$ when its speed is
1. $c$
2. $\frac{c\sqrt{3}}{2}$
3. $c\sqrt{3}$
4. $2c$
Relativistic mass is given by $m=\frac{m_0}{\sqrt{1-v^2/c^2}}$, substituting $m=2m_0$ and solving we get $v=\frac{c\sqrt{3}}{2}$

2. Twelve equal charges of magnitude $q$ are kept at the corners of a regular 12-sided polygon one at each of the corner. What is the net force on a test charge $Q$ at the center of the polygon at distance $r$?
1. Zero
2. $\frac{1}{4\pi\epsilon_0}\frac{12qQ}{r^2}$
3. $\frac{1}{4\pi\epsilon_0}\frac{6qQ}{r^2}$
4. $\frac{1}{4\pi\epsilon_0}\frac{qQ}{r^2}$
As charge $Q$ is placed at symmetric position the net force acting is zero.

3. Two equal charges each of magnitude $q$ are kept $d$ distance apart along X-axis. Now, the electric field at a distance $z(z>>d)$ above the midpoint between two charges is given by:

1. $E_z=\frac{1}{4\pi\epsilon_0}\frac{2q}{z^2}$
2. $E_z=\frac{1}{4\pi\epsilon_0}\frac{q^2}{z^2}$
3. $E_z=\frac{1}{4\pi\epsilon_0}\frac{2q}{r^{3/2}}$
4. $E_z=\frac{1}{4\pi\epsilon_0}\frac{2q}{(2+r)^2}$
Electric field at a point at a distance $z$ due to single charge is $E_1=\frac{1}{4\pi\epsilon_0}\frac{q}{r^2}$. Hence electric field at the same point along z-axis is $E_1=\frac{1}{4\pi\epsilon_0}\frac{q}{r^2}\cos\theta$. But $\cos\theta=\frac{z}{r}$ and $r=z^2+\frac{d^2}{4}$. Hence \begin{align*} E_1&=\frac{1}{4\pi\epsilon_0}\frac{q}{r^2}\frac{z}{r}\\ &=\frac{1}{4\pi\epsilon_0}\frac{qz}{r^3}\\ &=\frac{1}{4\pi\epsilon_0}\frac{qz}{(z^2+\frac{d^2}{4})^{3/2}} \end{align*} For $z>>d$, $\frac{d^2}{4}$ can be neglected. Hence,$E_1=\frac{1}{4\pi\epsilon_0}\frac{q}{z^2}$. Similarly, $E_2=\frac{1}{4\pi\epsilon_0}\frac{q}{z^2}$. Hence, $E=E_1+E_2=\frac{1}{4\pi\epsilon_0}\frac{2q}{z^2}$

4. Poynting's vector represent which of the following quantities?
   1. Current density vector producing electrostatic field
   2. Power density vector producing electromagnetic field
   3. Current density vector producing electromagnetic field
   4. Power density vector producing electrostatic and magnetostatic fields
   (B) Power density vector producing electromagnetic field.
   
5. An n-type semiconductor has an electron concentration of $3\times 10^{20} m^{-3}$. If the electron drift velocity is $100 ms^{-1}$ in an electric field of $200 Vm^{-1}$, the conductivity (in $\Omega m^{-1}$)
   1. 24
   2. 36
   3. 48
   4. 96
   Mobility $$\mu=\frac{v_d}{E}$$ Conductivity \begin{align*}\sigma&=n_e e\mu\\&=\frac{n_e e v_d}{E}\\&=\frac{3\times 10^{20}\times1.6\times 10^{-19}\times100}{200}\\&=24\end{align*}

Problem set 10

1. The function $f(z)=u(x,y)+iv(x,y)$ is analytic at $z=x+iy$. The value of $\nabla^2u$ at this point is:
1. 0
2. undefined
3. $\pi$
4. $e^{-\pi^2}$
The function $f(z)=u(x,y)+iv(x,y)$ is analytic at $z=x+iy$ means $u(x,y)$ and $v(x,y)$ satisfy Cauchy-Reiman equations namely $$\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}$$ $$\frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}$$ $$\therefore\nabla^2u=\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}$$ $$\nabla^2u=\frac{\partial }{\partial x}\left(\frac{\partial u}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{\partial u}{\partial y}\right)$$ \begin{align*} \nabla^2u&=\frac{\partial }{\partial x}\left(\frac{\partial v}{\partial y}\right)-\frac{\partial }{\partial y}\left(\frac{\partial v}{\partial x}\right)\\ &=\frac{\partial^2 v}{\partial x\partial y}-\frac{\partial^2 v}{\partial y\partial x}=0 \end{align*}
2. A head of mass $m$ slides on a smooth rod which is rotating about one end in a vertical plane with uniform angular velocity $\omega$. The Lagrangian of the system is :
1. $L=\frac{1}{2}m\left(\dot r^2+r^2\dot\theta^2\right)-mgr\sin\theta$
2. $L=\frac{1}{2}m\left(r^2\dot\theta^2\right)-mgr\sin\theta$
3. $L=\frac{1}{2}m\left(\dot r^2+\dot\theta^2\right)-mgr\sin\theta$
4. $L=\frac{1}{2}m\left(r^2\dot\theta^2\right)+mgr\sin\theta$
Kinetic energy of head due to sliding on the rod =$\frac{1}{2}m\dot r^2$

Kinetic energy of head due to rotation=$\frac{1}{2}mr^2\dot\theta^2$

Potential energy of the head due to vertical height=$mgr\sin\theta$ $$L=\frac{1}{2}m\left(\dot r^2+r^2\dot\theta^2\right)-mgr\sin\theta$$

3. A partition function of two Bose particles each of which can occupy any of the two energy levels $0$ and $\epsilon$ is
1. $1+e^{-2\epsilon/kT}+2e^{-\epsilon/kT}$
2. $1+e^{-2\epsilon/kT}+e^{-\epsilon/kT}$
3. $2+e^{-2\epsilon/kT}+e^{-\epsilon/kT}$
4. $e^{-2\epsilon/kT}+e^{-\epsilon/kT}$
The partition function for Bose particles is given by $Z=\sum\limits_Re^{-(n_1\epsilon_1+n_2\epsilon_2+\dots)/kT}$, where $n_1$ is number of particles with energy $\epsilon_1$ and so on. Bose particles are indistinguishable particles and any number of particles can be in any state. Hence states of the system can be obtained as follow.
Single particle energy	0	$\epsilon$
	AA
		AA
	A	A
\begin{align*} Z&=e^{-(2\times0)/kT}+e^{-(2\times\epsilon)/kT}\\ &+e^{-(1\times0+1\times\epsilon)/kT}\\ &=1+e^{-2\epsilon/kT}+e^{-\epsilon/kT} \end{align*}
4. A one dimensional random walker takes steps to left or right with equal probability. The probability that the random walker starting from origin is back to origin after $N$ even number of steps is
   1. $\frac{N!}{\left(\frac{N}{2}\right)!\left(\frac{N}{2}\right)!}\left(\frac{1}{2}\right)^N$
   2. $\frac{N!}{\left(\frac{N}{2}\right)!\left(\frac{N}{2}\right)!}$
   3. $2N!\left(\frac{1}{2}\right)^{2N}$
   4. $N!\left(\frac{1}{2}\right)^N$
   The probability $p(m,N)$ that the particle will be at the position $x = ml$ after $N$ steps is given by $${\scriptstyle p(m,N)=\frac{N!}{\left(\frac{N+m}{2}\right)!\left(\frac{N-m}{2}\right)!}p^{\frac{1}{2}\left(N+m\right)}q^{\frac{1}{2}\left(N-m\right)}}$$ Here $p=q=\frac{1}{2}$, the probability of taking steps to right and left, $l$ is step length and $x=ml=0$. Hence $m=0$. Hence $$p(0,N)=\frac{N!}{\left(\frac{N}{2}\right)!\left(\frac{N}{2}\right)!}\left(\frac{1}{2}\right)^N$$
5. Five electrons (Fermions with spin $1/2\hbar$) are kept in a one-dimensional infinite potential well with width $a$. (Ground state energy of single electron well $=\frac{\hbar^2\pi^2}{2ma^2}$). The first absorption line corresponds to energy:
   1. $\frac{\hbar^2\pi^2}{2ma^2}$
   2. $\frac{5\hbar^2\pi^2}{2ma^2}$
   3. $\frac{7\hbar^2\pi^2}{2ma^2}$
   4. $\frac{11\hbar^2\pi^2}{2ma^2}$
   As electrons are fermions, there can be two electrons with same energy. Hence ground state configuration will be two electrons in $n=1$ state, two electrons in $n=2$ state and one electron in $n=3$ state. The first absorption line corresponds to transition of electron from $n=3$ state to $n=4$ state. Energy of $n=3$ state is $\frac{9\hbar^2\pi^2}{2ma^2}$ and energy of $n=4$ state is $\frac{16\hbar^2\pi^2}{2ma^2}$. Hence first absorption line corresponds to energy $\frac{16\hbar^2\pi^2}{2ma^2}-\frac{9\hbar^2\pi^2}{2ma^2}=\frac{7\hbar^2\pi^2}{2ma^2}$

Problem set 9

1. The position vector $\bar r=x\hat i+y\hat j+z\hat k$, $\bar\nabla.\left(r^2\bar r\right)$ is given by:
1. 0
2. $5r^2$
3. $r^2$
4. $3r^2$
$r^2=x^2+y^2+z^2$ $${\scriptscriptstyle\bar\nabla.\left(r^2\bar r\right)=\left(\hat i\frac{\partial}{\partial x}+\hat j\frac{\partial}{\partial y}+\hat k\frac{\partial}{\partial x}\right)\cdot\left(\left(x^2+y^2+z^2\right)\left(x\hat i+y\hat j+z\hat k\right)\right)}$$ $$\bar\nabla.\left(r^2\bar r\right)=5r^2$$
2. The eigenvalues of the matrix: $\begin{pmatrix}1&2&3\\0&4&7\\0&0&3\end{pmatrix}$ are:
   1. 1, 4, 3
   2. 3, 7, 3
   3. 7, 3, 2
   4. 1, 2, 3
   In upper or lower triangular matrix, eigenvalues are the diagonal elements, Hence (A)1, 4, 3
3. Two solid spheres of radius $R$ and mass $M$ each are connected by a thin rod of negligible mass. The distance between the centres is $4R$. The moment of inertia about an axis passing through the centre of symmetry and perpendicular to the line joining the spheres is
1. $\frac{11}{5}MR^2$
2. $\frac{22}{5}MR^2$
3. $\frac{44}{5}MR^2$
4. $\frac{88}{5}MR^2$

MI of system= MI of sphere 1 about an axis through centre of symmetry +MI of sphere 2 about an axis through centre of symmetry

According to theorem of parallel axes MI of sphere 1 about an axis through centre of symmetry = MI of sphere 1 about an axis through its centre and parallel to axis through centre of symmetry + M X square of distance between axes. $$I_1=\frac{2}{5}MR^2+M(2R)^2=\frac{22}{5}MR^2$$ Similarly $$I_2=\frac{2}{5}MR^2+M(2R)^2=\frac{22}{5}MR^2$$ $$I=\frac{44}{5}MR^2$$
4. All solutions of the equation $e^z=-3$ are
1. $z=\ln \pi\ln 3,~n=\pm1,\pm2,\dots$
2. ${\scriptstyle z=\ln 3+i(2n+1)\pi,~n=0,\pm1,\pm2,\dots}$
3. ${\scriptstyle z=\ln 3+i~2n\pi,~n=0,\pm1,\pm2,\dots}$
4. $z=i3n\pi,~n=\pm1,\pm2,\dots$
Finding all solutions means to find all values of $z$ which will satify $e^z=-3$ \begin{align*} e^z&=-3\\ &=3(-1)\\ &={\scriptstyle3\left[\cos{(2n+1)\pi}+i\sin{(2n+1)\pi}\right]}\\ &=3e^{i(2n+1)\pi} \end{align*} Taking log on both sides we get $$z=\ln 3+i(2n+1)\pi~~~n=0,\pm1,\pm2,\dots$$
5. The solution of $\frac{dy}{dx}-y=e^{\lambda x}$ is :
1. $e^{-\lambda x}$
2. $\frac{1}{\lambda-1}e^{\lambda x}$
3. $e^{\lambda x}$
4. $\frac{1}{\lambda}e^{-\lambda x}$
Just by inspection or substituting $y=\frac{1}{\lambda-1}e^{\lambda x}$ in above equation one can verify that it is the solution. OR
The solution of $\frac{dy}{dx}+p(x)y=q(x)$ is given by $$y=\frac{\int u(x)q(x)dx+C}{u(x)}$$ where, $u(x)=exp\left(\int p(x)dx\right)$
Here $p(x)=-1$ and $q(x)=e^{\lambda x}$ $$u(x)=exp\left(-\int dx\right)=e^{-x}$$ \begin{align*} y&=\frac{\int e^{-x}e^{\lambda x}dx+C}{e^{-x}}\\ &=\frac{ e^{(\lambda-1) x}dx+C}{(\lambda-1)e^{-x}}\\ &=\frac{1}{\lambda-1}e^{\lambda x} \end{align*}

Problem set 8

1. The 623.8 nm radiation emitted by a He-Ne laser due to the transition between :
1. $3s$ and $2p$ levels of Ne
2. $3s$ and $3p$ levels of Ne
3. $2p$ and $2s$ levels of Ne
4. $2p$ and $1s$ levels of Ne
(A)$3s$ and $2p$ levels of Ne
2. In the Stern-Gerlach experiment, the number of components in which the atomic beam splits depends upon the value of:
1. $l$
2. $s$
3. $j$
4. $m_j$
(C)$j$
3. The Lande's splitting factor for the atomic state $^2P_{3/2}$ is :
1. $1/3$
2. $2/3$
3. $1$
4. $4/3$
For $^2P_{3/2}$ state $(2s+1)=2$, hence $s=1/2$, $j=3/2$, for $P$ state $l=1$ \begin{align*} g&={\scriptstyle1+\frac{j(j+1)+s(s+1)-l(l+1)}{2j(j+1)}}\\ &={\scriptstyle1+\frac{\frac{3}{2}(\frac{3}{2}+1)+\frac{1}{2}(\frac{1}{2}+1)-1(1+1)}{2\frac{3}{2}(\frac{3}{2}+1)}}\\ &=\frac{4}{3} \end{align*}
4. The "Normal" and "Anomalous" Zeeman effects are observed when (here S' is the total spin angular momentum due to the coupling of individual spin angular momenta)
1. $S'=0$ and $S'\ne0$, respectively
2. $S'=0$ and $S'=0$, respectively
3. $S'\ne0$ and $S'=0$, respectively
4. $S'\ne0$ and $S'\ne0$, respectively
(A)$S'=0$ and $S'\ne0$, respectively
5. The number of photons emitted per second from 1 watt Ar-ion laser operating at 488 nm is approximately
1. $10.23\times10^{19}$
2. $2.46\times10^{18}$
3. $10.23\times10^{17}$
4. $2.46\times10^{15}$
$Power=P=1 watt$, $\lambda=488 ~nm=488\times10^{-9}m$ $$P=NE=Nh\nu=N\frac{hc}{\lambda}$$ \begin{align*} N&=P\frac{\lambda}{hc}\\ &=1\times\frac{488\times10^{-9}}{6.63\times10^{-34}\times3\times10^8}\\ &=2.46\times10^{18} \end{align*}

Problem set 7

1. For a face centred cubic crystalline structure the following diffraction peaaks may be observed in the X-ray diffraction experiment:
1. (110), (330)
2. (111), (321)
3. (100), (321)
4. (111), (331)
For FCC structure- The peaks for which all h,k, l are even or all h,k, l are odd are present.
For BCC structure- The peaks for which h+k+l=even, are present.
For SCstructure- All peaks are present
Hence answer is (D)(111), (331)
2. In the X-ray diffraction of a set of crystal planes having $'d'$ equal to 0.18 nm, a first order reflection is found to be at an angle of $12^o$. The wavelength of X-ray used is [Given: $\sin{12^o}=0.2079$]
1. 0.1543 nm
2. 0.0749 nm
3. 0.0374 nm
4. 0.749 nm
Bragg's law is $$2d\sin\theta=n\lambda$$ For first order pattern $n=1$ \begin{align*} \lambda&=2\times0.18\times10^{-9}\sin12^o\\ &=2\times0.18\times10^{-9}\times0.2079\\ &=0.0749 nm \end{align*}
3. The outer electron configuration of divalent Manganese ion is $3d^54s^0$. The ground state of this ion is characterized by the spectroscopic term:
1. $^6S_{5/2}$
2. $^2D_{5/2}$
3. $^2F_{5/2}$
4. $^6H_{5/2}$
The rules governing the term symbol for the ground state according to L-S coupling scheme are given below:
1. The spin multiplicity is maximized i.e., the electrons occupy degenerate orbitals so as to retain parallel spins as long as possible (Hund’s rule).
2. The orbital angular momentum is also maximized i.e., the orbitals are filled with highest positive m values first.
3. If the sub-shell is less than half-filled, $J = L– S$ and if the sub-shell is more than half – filled, $J = L +S$.
The term symbol is given by $^{2S+1}L_J$. The left-hand superscript of the term is the spin multiplicity, given by $2S+1$ and the right- hand subscript is given by $J$.
For $d^5$ configuration we have
	$\uparrow$	$\uparrow$	$\uparrow$	$\uparrow$	$\uparrow$
$m_l=$	+2	+1	0	-1	-2
Hence, \begin{align*} L&={\scriptstyle(+2)+(+1)+(0)+(-1)+(-2)}\\ &=0 \end{align*} i.e. $S$ state \begin{align*} S&={\scriptstyle(+1/2)+(+1/2)+(+1/2)+(+1/2)+(+1/2)}\\ &=5/2 \end{align*} $$2S+1=6$$ $$J=L+S=0+5/2=5/2$$ Term symbol is $^6S_{5/2}$
4. Consider a nuclear $F^{19}$. When it is placed in a magnetic field of 1.0 tesla, the resonance frequency (in units of MHz) of the signal observed for this nucleus in the NMR spectrometer is : (Given: $g_N=5.256$, $\mu_N=5.0504\times10^{-27} J/T$; the subscript $N$ refers to the nuclear factors)
1. 30 MHz
2. 90 MHz
3. 40 MHz
4. 5.0 MHz
The resonance condition for NMR is $$h\nu=g_N\mu_NB_0$$ \begin{align*} \nu&=\frac{g_N\mu_NB_0}{h}\\ &=\frac{5.256\times5.0504\times10^{-27}\times1}{6.626\times10^{-34}}\\ &=40~MHz \end{align*}
5. The work done in bringing a charge $+q$ from infinity in free space, to a position at a distance $d$ in front of a semi-infinite grounded metal surface is
1. $-\frac{q^2}{4\pi\epsilon_0(d)}$
2. $-\frac{q^2}{4\pi\epsilon_0(2d)}$
3. $-\frac{q^2}{4\pi\epsilon_0(4d)}$
4. $-\frac{q^2}{4\pi\epsilon_0(6d)}$
In front of a semi-infinite grounded metal surface when a charge $q$ is held at a distance $x$, then there is an image charge $-q$ at a distance $x$ behind the metal surface. Hence force on $+q$ charge is given by $$F=-\frac{q^2}{4\pi\epsilon_0(2x)^2}$$ Hence force required to move the charge is $$F=\frac{q^2}{4\pi\epsilon_0(2x)^2}$$ \begin{align*} W&=\int_{\infty}^{d}Fdx\\ &=\frac{q^2}{4\pi\epsilon_0(4)}\int_{\infty}^d\frac{1}{x^2}dx\\ &=-\frac{q^2}{4\pi\epsilon_0(4d)} \end{align*}

Problem set 6

1. If the electrostatic potential were given by $\phi=\phi_0\left(x^2+y^2+z^2\right)$, where $\phi_0$ is constant, then the charge density giving rise to the above potential would be
1. 0
2. $-6\phi_0\epsilon_0$
3. $-2\phi_0\epsilon_0$
4. $-\frac{6\phi_0}{\epsilon_0}$
\begin{align*} \bar E&=-\bar \nabla\phi\\ &=-\bar \nabla\left\{\phi_0\left(x^2+y^2+z^2\right)\right\}\\ &=-2\phi_0(x\hat i+y\hat j+z\hat k) \end{align*} Charge density $\sigma=\epsilon_0\bar\nabla.\bar E=-6\phi_0\epsilon_0$
2. A set of 15 distinguishable particles are placed in 3 energy states such that 2 particles in the first state, 12 in the second state and 1 in the third state. The number of distinct arrangements are:
1. 1365
2. 15
3. 455
4. $3^{15}$
Number of ways of arranging $N$ distinguishable particles into groups of $N_j$ each, such that $N_1$ in state 1, $N_2$ in state 2, etc. and $N_j$ in the $j^{th}$ state are given by $$W(N)=\frac{N!}{N_1!N_2!\dots N_j!}$$ $$W(15)=\frac{15!}{2!\times12!\times1!}=1365$$
3. The critical temperature for the Bose-Einstein condensation depends on the density of particles as :
   1. $n^{1/3}$
   2. $n^{2/3}$
   3. $n$
   4. $n^{1/2}$
   $N=\frac{V(2\pi mkT)^{3/2}}{h^3}2.162$. Hence (B)$n^{2/3}$
4. In $^3S$ state of the Helium atom, the possible values of the total electronic angular momentum quantum numbers are:
   1. 0 (zero) only
   2. 1 only
   3. 0,1 and 2
   4. 0 and 1 only
   The term symbol is given by $^{(2s+1)}L_J$. For $^3S$ state $(2s+1)=3$, hence $s=1$. For $S$ state $L=0$. Hence $J=L+S=1$. Hence answer is (B)1 only
5. The probability that two friends have the same birth month is:
1. $\frac{1}{6}$
2. $\frac{1}{12}$
3. $\frac{1}{36}$
4. $\frac{1}{144}$
A person can have birthday in any of the 12 months of the year. Another person can also have his/her birthday in any of the 12 months. Now,the total number of possible combinations is 12*12 , which equals 144. This set of all possible combinations contains 12 pairs of identical months {for example(Jan,Jan)}, which are our favourable outcomes.
Thus the probability =
(Number of favourable outcomes)/(Number of events in sample space)=12/(12*12)=1/12

Problem set 5

1. A planet moves around the sun in an elliptic orbit with length of major axis equal to 1.524 times that of the Earth. The time of revolution of the planet about the Sun is
1. 1 year
2. 10.24 year
3. 0.5315 year
4. 1.8814 year
According to Kepler's third law, the square of the orbital period of a planet is proportional to the cube of the semi-major axis of its orbit. Hence, period of revolution of a planet around the Sun in an elliptic orbit is given by $$T^2=K_sa^3$$, where $K_s=2.97\times10^{-19}s^2/m^3$. $$T^2_{earth}=K_sa^3_{earth}$$ $$T^2_{planet}=K_sa^3_{planet}$$ $$\frac{T^2_{planet}}{T^2_{earth}}=\frac{a^3_{planet}}{a^3_{earth}}$$ $$\frac{T^2_{planet}}{1}=\frac{\left(1.524a_{earth}\right)^3}{a^3_{earth}}$$ $$T_{planet}=\left(1.524\right)^{3/2}=1.8814~ years$$
2. A particle is released from a large height $h$, at a location with latitude $\lambda$. At the time of striking the ground, the horizontal deflection that occurs due to Coriolis force, is proportional to
1. $\sin{\lambda}$
2. $\cos{\lambda}$
3. $\sec{\lambda}$
4. $cosec\lambda$
The horizontal deflection is given by $$y(h)=\frac{2h\omega\sin\theta}{3}\sqrt{\frac{2h}{g}}$$ where $\theta$ is colatitude. If $\lambda$ is latitude then $\sin\theta=cos\lambda$ $$y(h)=\frac{2h\omega\cos\lambda}{3}\sqrt{\frac{2h}{g}}$$
3. The centre of the circle $\bar z z+(2+3i)\bar z+(2-3i)z+1=0$ is
   1. (2,3)
   2. (3,2)
   3. (-2,-3)
   4. (4,0)
   Let $z=x+iy$ \begin{align*} \therefore \bar z z+(2+3i)\bar z+(2-3i)z+1\\ =(x-iy)(x+iy)+(2+3i)(x-iy)\\+(2-3i)(x+iy)+1\\ =x^2+y^2+2x-2iy+3ix+3y\\+2x+2iy-3ix+3y+1\\ =x^2+y^2+4x+6y+1 \end{align*} $$\therefore\bar z z+(2+3i)\bar z+(2-3i)z+1=0$$ gives $$(x+2)^2+(y+3)^2-12=0$$ $(x+2)^2+(y+3)^2=12$ is equation of circle with centre $(-2,-3)$ and radius $\sqrt{12}$
4. Fourier transform of the function $f(x)=exp(-|x|)$ is
   1. $\frac{1}{\sqrt{2\pi}}\left[\frac{2}{1+k^2}\right]$
   2. $0$
   3. $\frac{1}{\sqrt{\pi}}\left[\frac{1}{k^2}\right]$
   4. $\frac{1}{\sqrt{2\pi}}\left[\frac{1}{1-k^2}\right]$
   $|x|=x$ if $x>0$ and $|x|=-x$ if $x<0$. Fourier transform of $f(x)$ is given by $$F(k)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}e^{-ikx}f(x)dx$$ \begin{align*} F(k)={\scriptstyle\frac{1}{\sqrt{2\pi}}\left[\int_{-\infty}^{0}e^{-ikx}e^xdx+\int_{0}^{\infty}e^{-ikx}e^{-x}dx\right]} \end{align*} $$F(k)={\scriptstyle\frac{1}{\sqrt{2\pi}}\left[\int_{-\infty}^{0}e^{x(1-ik)}dx+\int_{0}^{\infty}e^{-x(1+ik)}dx\right]}$$ $$F(k)=\frac{1}{\sqrt{2\pi}}\left[\frac{2}{1+k^2}\right]$$
5. The area of the triangle whose base is given by $\bar a=5\hat i-3\hat j+4\hat k$ and $\bar b=\hat j-\hat k$ is another side is :
   1. $\sqrt{50}/2$
   2. $\sqrt{61}/2$
   3. $\sqrt{14}/2$
   4. $\sqrt{51}/2$
   \begin{align*} &\text{Area of triangle }=\frac{1}{2}|\bar a\times\bar b|\\ &=\frac{1}{2}|-\hat i+5\hat j+5\hat k|=\sqrt{51}/2 \end{align*}

Problem set 4

1. For a system performing small oscillations, which of the following statement is correct?
1. The number of normal modes and the number of normal coordinates is equal
2. The number of normal modes is twice the number of normal coordinates
3. The number of normal modes is half the number of normal coordinates
4. There is no specific relationship between the number of normal modes and the number of normal coordinates
(A) The number of normal modes and the number of normal coordinates is equal.
2. For any process, the second law of thermodynamics requires that the change of entropy of the universe be
1. Positive only
2. Positive or zero
3. Zero only
4. Negative or zero
(B) because for reversible process entropy is zero and for irreversible process entropy is positive
3. A body of mass $M=m_1+m_2$ at rest splits into two parts of masses $m_1$ and $m_2$ by an internal explosion which generates a kinetic energy $E$. The speed of mass $m_2$ relative to mass $m_1$ is
1. $\sqrt{\frac{E}{m_1m_2}}$
2. $\sqrt{\frac{2E}{m_1m_2}}$
3. $\sqrt{\frac{EM}{m_1m_2}}$
4. $\sqrt{\frac{2EM}{m_1m_2}}$
After explosion let two parts moves with velocities $v_1$ and $v_2$. According to law of conservation of momentum, the total momentum after split equal to the total momentum before split. i.e. $$m_1v_1+m_2v_2=0M$$ Kinetic energy generated is given by $$E=\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2-\frac{1}{2}M0^2$$ $$E=\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2$$ \begin{align*} 2E&=m_1v_1^2+m_2v_2^2\\ &=-m_2v_2v_1+m_2v_2^2\\ &=m_2\left(v_2^2-v_1v_2\right) \end{align*} \begin{align*} 2E&=m_1v_1^2+m_2v_2^2\\ &=m_1v_1^2-m_1v_1v_2\\ &=m_1\left(v_1^2-v_1v_2\right) \end{align*} $$\frac{2E}{m_2}=\left(v_2^2-v_1v_2\right)$$ $$\frac{2E}{m_1}=\left(v_1^2-v_1v_2\right)$$ Adding these two equations we get $$\frac{2EM}{m_1m_2}=\left(v_1^2+v_2^2-2v_1v_2\right)$$ $$\sqrt{\frac{2EM}{m_1m_2}}=\left(v_2-v_1\right)$$
4. The value of $$x=1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\dots} }}$$
1. $\sqrt{2}$
2. 1.6
3. $\sqrt{3}$
4. 0.8
\begin{align*} x&=1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\dots} }}\\ &=1+\frac{1}{x} \end{align*} $$x^2-x-1=0$$ $$x=\frac{1\pm\sqrt{1+4}}{2}=1.6$$
5. In Young's double slit experiment, if one of the following parameters ($\lambda$, $d$ and $D$) is increased in the same order keeping the other two same, then the fringe width
1. decreases, decreases, increases
2. decreases, increases, increases
3. increases, decreases, increases
4. increases, increases, decreases
Fringe width is the distance between two fringes of the same kind. The formula for fringe width is $\Delta y=\frac{\lambda D}{d}$ If we increase $\lambda$ the fringe width increases. If we increase $d$ the fringe width decreases. If we increase $D$ the fringe width increases. Hence answer is (C)
6. Ideal Atwood machine is nothing but an inextensible string of negligible mass going around the fixed pulley with masses $m_1$ and $m_2$ attached to the ends of the string. If $m_1>m_2$, then the magnitude of acceleration of mass $m_1$ is
1. $\frac{m_1g}{(m_1+m_2)}$
2. $\frac{m_2g}{(m_1+m_2)}$
3. $\frac{(m_1-m_2)g}{(m_1+m_2)}$
4. $g$
Let us take upward direction as positive and downward direction as negative. Force on mass $m_1$ is $$T-m_1g=-m_1a_1$$ Force on mass $m_2$ is $$T-m_2g=m_2a_2$$ $$m_1a_1=m_1g-T$$ $$m_2a_2=T-m_2g$$ $$m_1a_1+m_2a_2=m_1g-m_2g$$ But $a_1=a_2=a$ $$a=\frac{(m_1-m_2)g}{(m_1+m_2)}$$
7. A particle of mass $m$ is released from a large height. Resistive force is directly proportional to velocity $\bar v$ with $k$ as a constant of proportionality. Asymptotic value of the velocity of particle is
1. $\frac{g}{k}$
2. $\frac{k}{m}$
3. $\frac{mg}{k}$
4. $\frac{g}{km}$
Let us take downward direction as positive. Hence force acting on particle is given by $$F=ma=mg-kv$$ $$\frac{dv}{dt}=g-\frac{k}{m}v$$ Asymptotic value of $v$ is the terminal velocity $v_t$, which is constant. Hence, $\frac{dv_t}{dt}=0$ $$g-\frac{k}{m}v_t=0$$ $$v_t=\frac{mg}{k}$$
8. The momentum of an electron (rest mass $m_0$), which has the same kinetic energy as its rest mass energy, is
1. $m_0c$
2. $\sqrt{2}m_0c$
3. $\sqrt{3}m_0c$
4. $2m_0c$
Energy of electron is given by $$E=mc^2=\sqrt{p^2c^2+m_0^2c^4}$$. Also \begin{align*} E&=mc^2\\ &=KE+Rest~mass~energy\\ &=KE+m_0c^2=2m_0c^2 \end{align*} $$2m_0c^2=\sqrt{p^2c^2+m_0^2c^4}$$ $$4m_0^2c^4=p^2c^2+m_0^2c^4$$ $$p^2c^2=3m_0^2c^4$$ $$p=\sqrt{3}m_0c$$
9. A planet of mass $m$ moves around the in an elliptic orbit. If $L$ denotes the angular momentum of the planet, then the rate at which area is swept by the radial vector is
1. $\frac{L}{2m}$
2. $\frac{L}{m}$
3. $\frac{2L}{2}$
4. $\frac{\sqrt{2}L}{m}$
(A)$\frac{L}{2m}$
10. The matrix $\begin{pmatrix}8&x&0\\4&0&2\\12&6&0\end{pmatrix}$ will become singular if the value of $x$ is
    1. $4$
    2. $6$
    3. $8$
    4. $12$
    If the matrix is singular, its determinant is zero. $$det=-96+24x=0$$ Hence, $x=4$